H2 Math Sun 2pm

By KS Teng

This page contains all questions and answers asked by students from this class. The most recent questions will be at the top.

MF26

Question 15 CJC/2013

Question 15 CJC/2013

LHS = \sum_{r=2}^n \frac{1}{(r+1)(r-1)}
= \sum_{r=2}^n \frac{1}{2} (\frac{1}{r-1} - \frac{1}{r+1})
= \frac{1}{2} \sum_{r=2}^n \frac{1}{r-1} - \frac{1}{r+1}
= \frac{1}{2} [\frac{1}{1} - \frac{1}{3}
+ \frac{1}{2} - \frac{1}{4}
+ \frac{1}{3} - \frac{1}{5}
…
+ \frac{1}{n-3} - \frac{1}{n-1}
+ \frac{1}{n-2} - \frac{1}{n}
+ \frac{1}{n-1} - \frac{1}{n+1}]
= \frac{1}{2} [\frac{3}{2} - \frac{1}{n} - \frac{1}{n+1}]
= \frac{3}{4} - \frac{1}{2n} - \frac{1}{2n+2}

Since the lim_{n \rightarrow \infty} \sum_{r=2}^n \frac{1}{(r+1)(r-1)}
= lim_{n \rightarrow \infty} \frac{3}{4} - \frac{1}{2n} - \frac{1}{2n+2}
= \frac{3}{4} - 0 - 0
- \frac{3}{4} is a constant, the series convergences.
The sum to infinity = \frac{3}{4}

Question 14a MJC/2013

Question 14a MJC/2013

Let T_n denote the n^{th} term of the AP.
T_n = a + (n-1)d
T_1 = a
T_3 = a +2d
T_6 = a +5d
Since they are consecutive terms of a GP,
\frac{T_3}{T_1} = \frac{T_6}{T_3} = r
\Rightarrow \frac{a+2d}{a} = \frac{a+5d}{a+2d}
(a+2d)^2 = a(a+5d)
a^2 + 4ad + 4d^2 = a^2 + 5ad
4d^2 - ad =0
d(4d - a) = 0
d = 0 (NA) \mathrm{~or~} 4d = a
\Rightarrow r = \frac{a+2d}{a}
r = \frac{6d+2d}{4d} = \frac{3}{2} > 1, thus its not convergent

S_{15} = \frac{n}{2}(2a + (n-1)d)
= \frac{15}{2}(2a + 14 (\frac{a}{4}))
= 41.25 a

Question 11 DHS/2013

Question 11 DHS/2013

Sum of first 3 terms = \frac{3}{2} (2a+(3-1)d)
6 = 3a+3d
a+d=2 —(1)
Sum of last 3 terms = \frac{3}{2}[2(a+(n-1)d) + (3-1)(-d)]; Here we consider an AP that has first term T_n = a + (n-1)d and common difference -d.
\Rightarrow 231 = \frac{3}{2}(2a + 2nd - 2d -2d)
231 = 3a + 3nd - 6d
77 = a + nd -2d —(2)
Sum of n terms = \frac{n}{2}[2a+ (n-1)d]
1106 = \frac{n}{2}(2a + nd - d) —(3)
Solve for n.

Question 12 SRJC/2012

Question 12 SRJC/2012

(i) Volume, V = \pi r^2 h
Volume of kth later, V_k = \pi [(20)(\frac{5}{6})^{k-1}]^2(22)(\frac{4}{5})^{k-1}
V_k = 8800 \pi [\frac{25}{36} \times \frac{4}{5}]^{k-1}
V_k = 8800 \pi (\frac{5}{9})^{k-1}
(ii)
Since r = \frac{5}{9} <1, S_{\infty} exists.
Theoretical Max Volume, S_{\infty} = \frac{8800 \pi}{1 - \frac{5}{9}} = 19800 \pi.
Total Volume, S_n = \frac{8800 \pi (1 - (\frac{5}{9})^n)}{1 - \frac{5}{9}}
We want S_n \le 0.95 S_{\infty}

Comments
    pingbacks / trackbacks
    • Class Q&A – The Culture

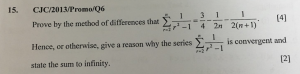
      […] Math Sat 130pm H2 Math Sat 330pm H2 Math Sun 930am H2 Math Sun 1130am H2 Math Sun 2pm H2 Math Mon 2pm H2 Math Mon 430pm H2 Math Mon 730pm H2 Math Tue 5pm H2 Math Tue 7pm H2 Math Thur […]

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    H2 Math Sun 1130amJC Mathematics
    H2 Math Mon 430pmJC Mathematics