Sampling & Survey #2 – Simple Probability Samples

So recall that we are interested on the statistical aspects of taking and analysing a sample, and a good sample will be representative in the sense that characteristics of interest in the population can be estimated form the sample with a known degree of accuracy.

Here, we will use Probability Sampling to conduct surveys. Probability sampling means each unit in the population has a known non-zero probability of being included in the sample. At the same time, we will make the following assumption:

1. Sampled population = target population
2. Sampling frame is complete, no non-response or missing data
3. No measurement error

Clearly, with these assumptions, we have removed non-sampling error and only observe sampling error.

Simple Random Sample

• Simplest form of probability sample
• Each unit has an equal probability to be in the sample
• Each sample of size n has the same chance of being the samples

Systematic Sample

• Units are equally spaced in the list

Stratified sample

• Elements in the same stratum often tend to be more similar.
• Simple random sample selected from each stratum, and sample random samples in the strata are selected independently

Cluster Sample

• Elements are aggregated into larger sampling units (cluster)
• The cluster is sampled:
  • One – stage (entire cluster is sampled)
  • Two – stage (probability sampling within the cluster)

So here is an example to sample 20 integers from the population {1, 2, …, 100} using the above methods

1. Simple random sample: Use a computer to randomly generate 20 integers from 1 to 100.
2. Systematic sample: Use a computer to randomly generate an integer from 1 to 5, then take every 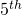element. Suppose it was 2, then the sample contains units 2, 7, 12, 17, …
3. Stratified sample: Divide the population into 10 strata, {1, 2, …, 10}, {11, 12, …, 20}, …, {91, 92, …, 100}, and a simple random sample of 2 numbers will be drawn from each of the 10 strata.
4. Cluster sample: Divide the population into 20 clusters {1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, …, {96, 97, 98, 99, 100}. A simple random sample of 4 of these clusters is selected.

Now we move on to developing some concepts and tools to analyse our sample.

For most samples, we are establish a characteristic of interest, y. Let be the characteristic of interest for unit i.

1. Population mean,
   
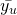
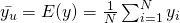
2. Population proportion, p
   This is a special population mean.
   Let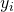 be binary variable, taking value of 1 if unit i have characteristic and 0 if unit i does not have characteristic.
   
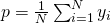
3. Population Total t
   
   
   
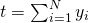
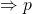
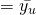
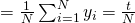
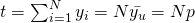
4. Population variance
   
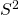
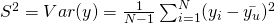
   S is the standard deviation of y.
5. Coefficient of variation CY(y)
   The coefficient of variation is a measure of relative variability; it is the ratio of the standard deviation of y with .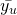
   

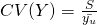
Next, we will delve deep into each of the sampling methods above.

Sampling & Survey #1 – Introduction
Sampling & Survey #2 – Simple Probability Samples
Sampling & Survey #3 – Simple Random Sampling
Sampling & Survey #4 – Qualities of estimator in SRS
Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS
Sampling & Survey #6 – Systematic Sampling
Sampling & Survey #7 – Stratified Sampling
Sampling & Survey # 8 – Ratio Estimation
Sampling & Survey # 9 – Regression Estimation
Sampling & Survey #10 – Cluster Sampling
Sampling & Survey #11 – Two – Stage Cluster Sampling
Sampling & Survey #12 – Sampling with unequal probabilities (Part 1)
Sampling & Survey #13 – Sampling with unequal probabilities (Part 2)
Sampling & Survey #14 – Nonresponse