2014 A-level H2 Mathematics (9740) Paper 1 Question 11 Suggested Solutions

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
$\mathrm{Vol}, V = \frac{2}{3} \pi r^{3} + \frac{1}{3} \pi r^{2}h$

Using Pythagoras’ Theorem, we have $h^{2}=4^{2}-r^{2}$

$V = \frac{2}{3} \pi r^{3} + \frac{1}{3} \pi r^{2} \sqrt{4^{2}-r^{2}}$

$\frac{dV}{dr} = 2 \pi r^{2} + \frac{1}{3} \pi [2r\sqrt{4^{2}-r^{2}}+(r^{2})(\frac{-r}{\sqrt{4^{2}-r^{2}}})]$

When $r=r_{1}, \frac{dV}{dr} = 0$ ,

$2 \pi r^{2} + \frac{1}{3} \pi [2r\sqrt{4^{2}-r^{2}}-(\frac{r^{3}}{\sqrt{4^{2}-r^{2}}})] = 0$

$2 \pi r^{2}\sqrt{4^{2}-r^{2}} + \frac{1}{3} \pi [2r(4^{2}-r^{2})-r^{3}] = 0$

$2 r^{2}\sqrt{16-r^{2}} + \frac{1}{3} [32r-2r^{3}-r^{3}] = 0$

$2 r^{2}\sqrt{16-r^{2}} + \frac{1}{3} (32r-3r^{3}) = 0$

$2 r^{2}\sqrt{16-r^{2}} = \frac{1}{3} (3r^{3}-32r)$

$6r\sqrt{16-r^{2}} = (3r^{2}-32)$

$[6r\sqrt{16-r^{2}}]^{2} = (3r^{2}-32)^{2}$

$36r^{2}(16-r^{2}) = 9r^{4}-192r^{2}+1024$

$45r^{4}-768r^{2}+1024=0$

(ii)
Using GC, $r=1.207 \text{~or~} r=3.951$

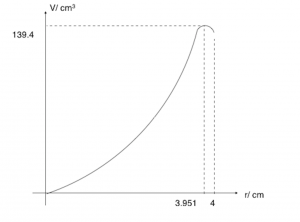
(iii)
When $r=1.207$ , using GC, $\frac{dV}{dr} = 18.3 \neq 0$

Thus, $r=1.207$ does not give a stationary value of $V$ .

When $r=3.951=r_1, ~ h=0.625$

(iv) Note than $r \textless 4$ ,

Graph for 11(iv)

Personal Comments:
It is rather disappointing to see some students unable to reach this question. Some panicked and differentiated wrongly, then forcefully copied what they were required to show. Students should also still continue with subsequent parts even if they cannot show (i). The interesting part of this question is that the last few parts require students to know how to use the GC effectively, in particularly setting the correct window for the graph in (iv) while (ii) and (iii) is entirely GC work as I’ve shown numerous times in classes.

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Comments

pingbacks / trackbacks

2014 H2 Mathematics (9740) Suggested Solutions | The Culture
[…] 2014 H2 Mathematics (9740) Paper 1 Question 11 Suggested Solutions […]
July 28th, 2015 06:42 PM

Cart

2014 A-level H2 Mathematics (9740) Paper 1 Question 11 Suggested Solutions

Leave a Comment
Cancel reply

2014 A-level H2 Mathematics (9740) Paper 1 Question 11 Suggested Solutions

Leave a Comment Cancel reply

Leave a Comment
Cancel reply