Hopefully, you guys have started on the Set A. You will find the following solutions useful. Click on the question. Please do attempt them during this December Holidays. 🙂
If you do have any questions, please WhatsApp me. 🙂
Firstly, either consider ![]() or square both sides. Its easier to do the latter (so I will).
or square both sides. Its easier to do the latter (so I will).
![]()
![]()
![]()
![]()
![]()
Since ![]() for all
for all ![]()
![]()
![]()
![]()
![]()
(i)
LHS
![]()
![]()
![]() RHS.
RHS.
(ii)
![]()
![]()
(Showing workings for Method of Difference)
![]()
(iii)
As ![]() .
.
Hence, the series converges to ![]() .
.
(i)
Let ![]()
![]() — (1)
— (1)
![]() — (2)
— (2)
![]() — (3)
— (3)
Using GC, ![]()
(ii)
![]()
![]()
![]()
![]()
![]()
![]()
Since arithmetic series is increasing, ![]() ,
,
![]()
Common ratio ![]()
Since ![]() , the geometric series converges.
, the geometric series converges.
(ii)
First term ![]()
![]()
![]()
By Pythagoras’ Theorem,
![]()
![]()
![]() since
since ![]()
Area, ![]()
![]()
Let ![]()
![]()
![]()
Check with first derivative test.
Hence, ![]() maximises A.
maximises A.
![]()
Thus, dimensions are ![]() m and
m and ![]() m (to 3.s.f.).
m (to 3.s.f.).
![]()
![]()
(i)
![]()
![]()
![]()
![]()
![]() , where
, where ![]() is an arbitrary constant.
is an arbitrary constant.
When ![]() .
.
![]()
(ii)
As ![]() .
.
Thus, the population of salmon in the fish farm will decrease towards 6,000 in the long run.
(a)
![]()
![]()
![]()
![]()
![]()
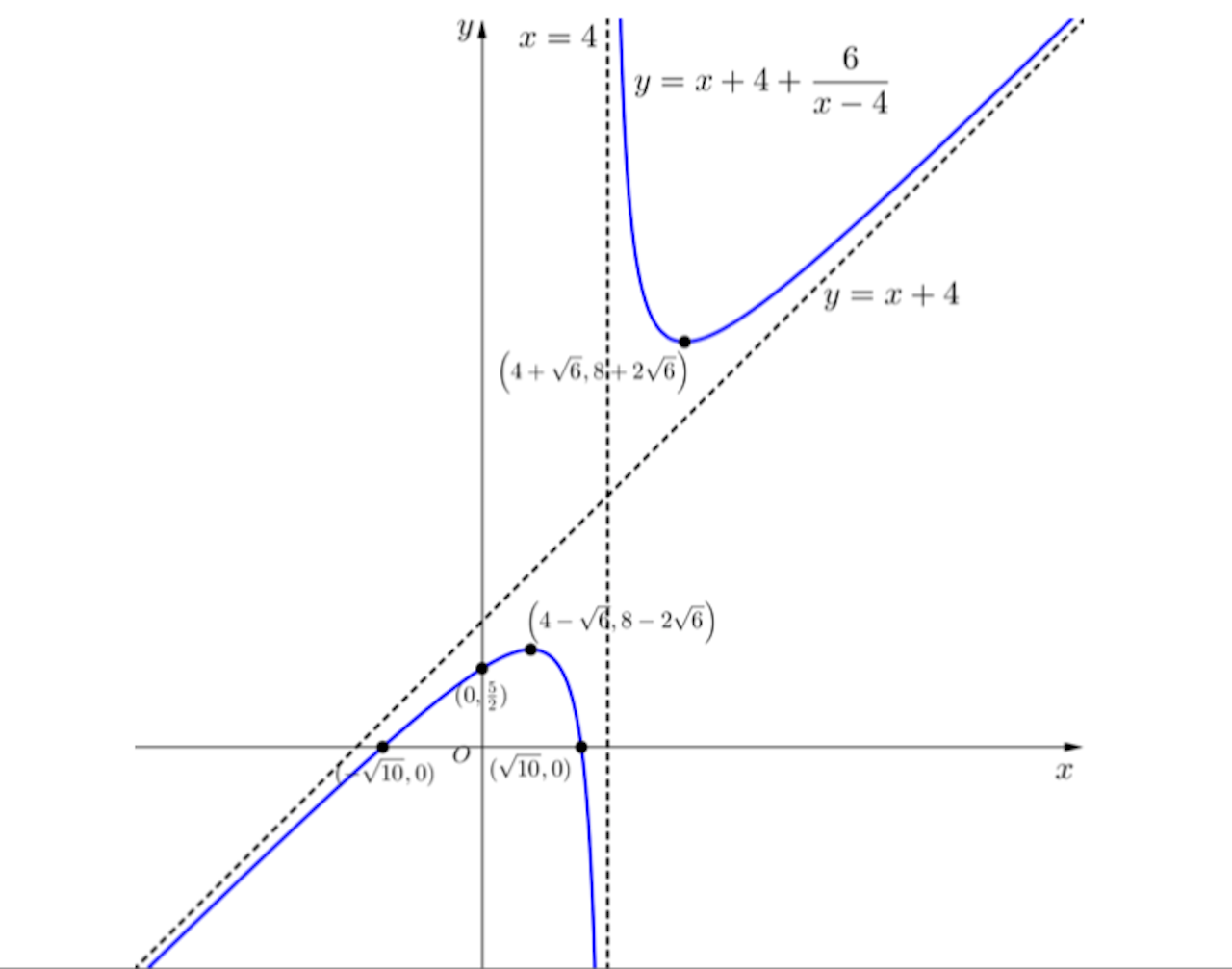
(b)
![]()
![]()
![]()
(c)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
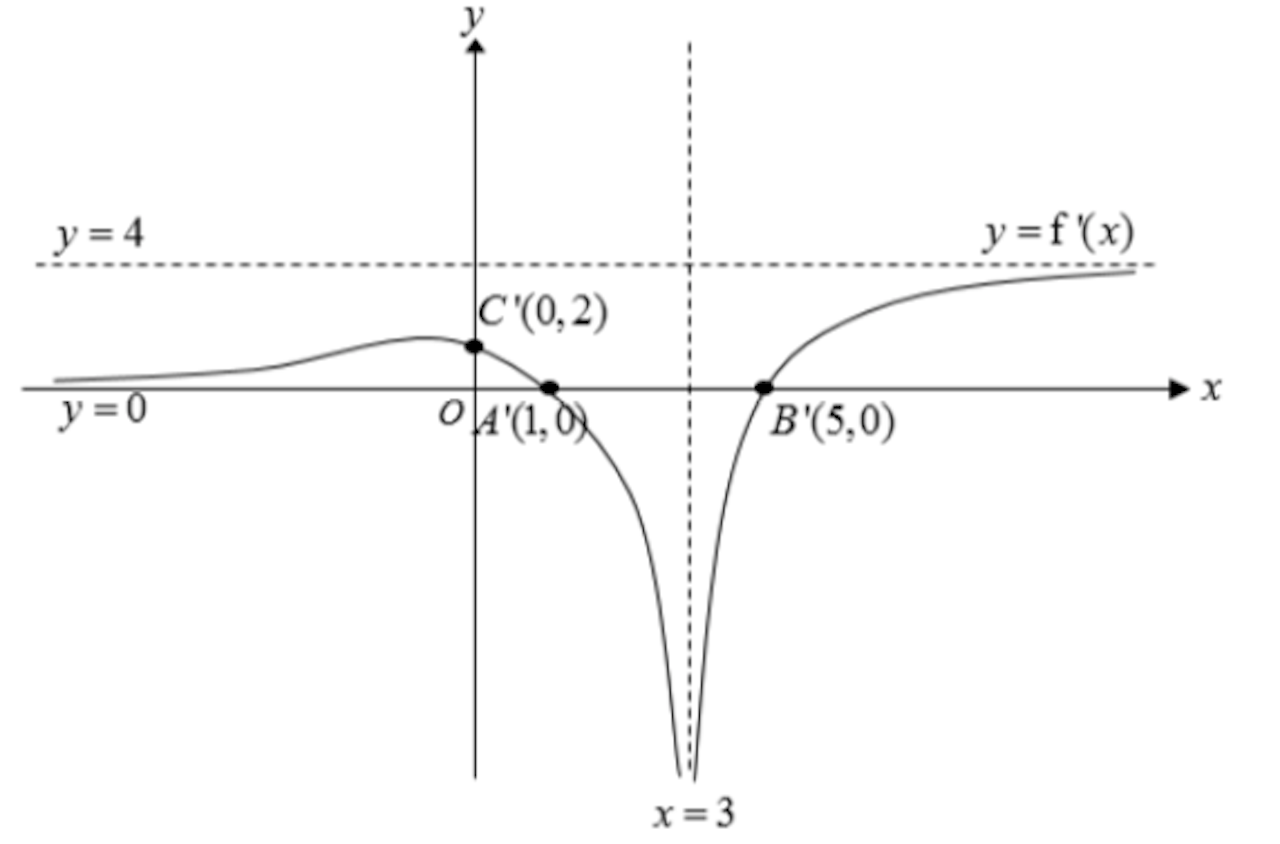
For curve to cut the x axis at 2 distinct points,
![]()
![]() or
or ![]()
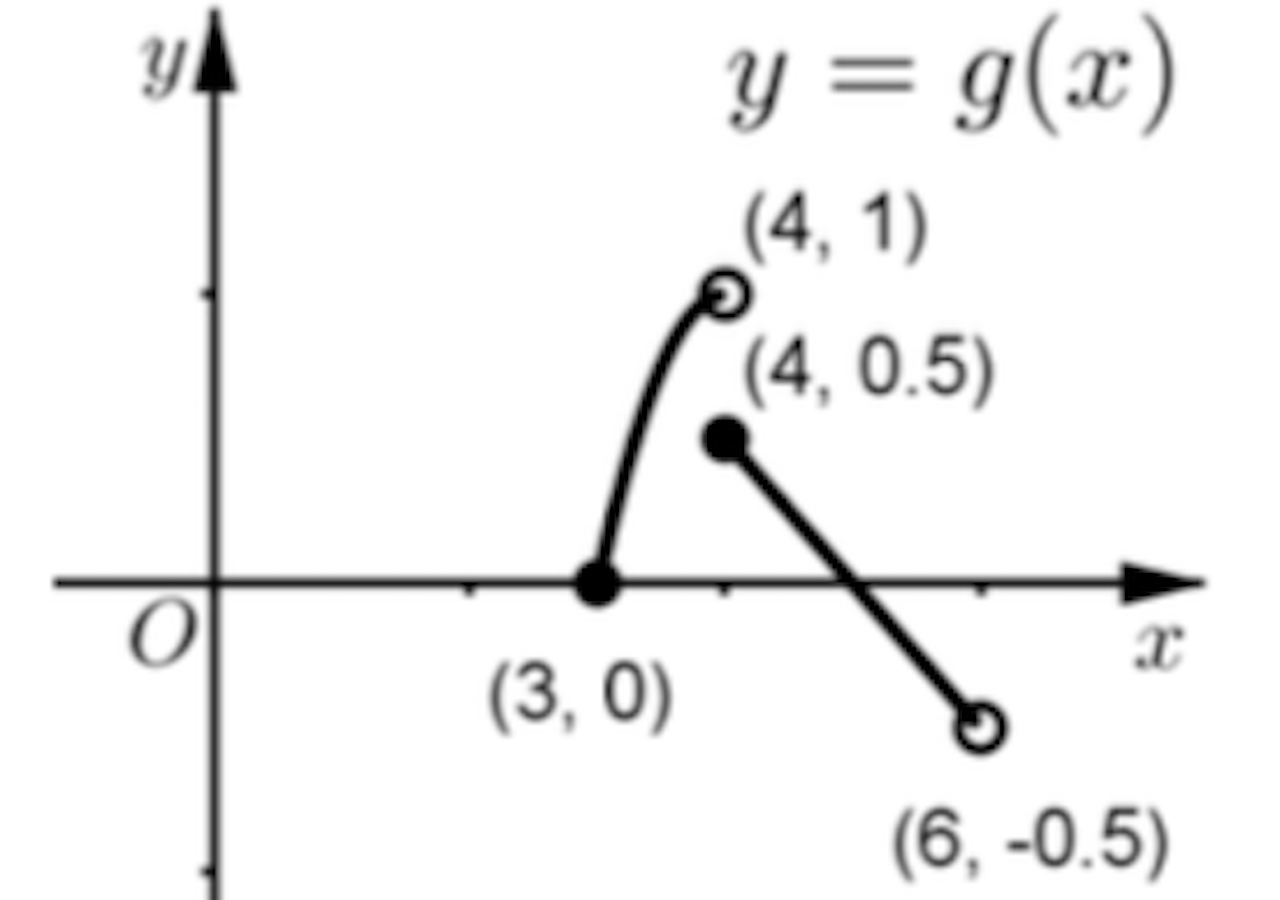
(i)
(ii)
![]() — (1)
— (1)
![]() — (2)
— (2)
Coordinate of ![]()
When ![]()
Observe that ![]() passes through
passes through ![]() for all real values of
for all real values of ![]() .
.
Thus, for line to not intersect C, ![]() .
.
(iii)
![]()
![]()
![]() or
or ![]()
(a)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(b)
(i)
![]()
![]()
![]()
![]()
(ii)
![]()
![]()
When ![]()
![]()
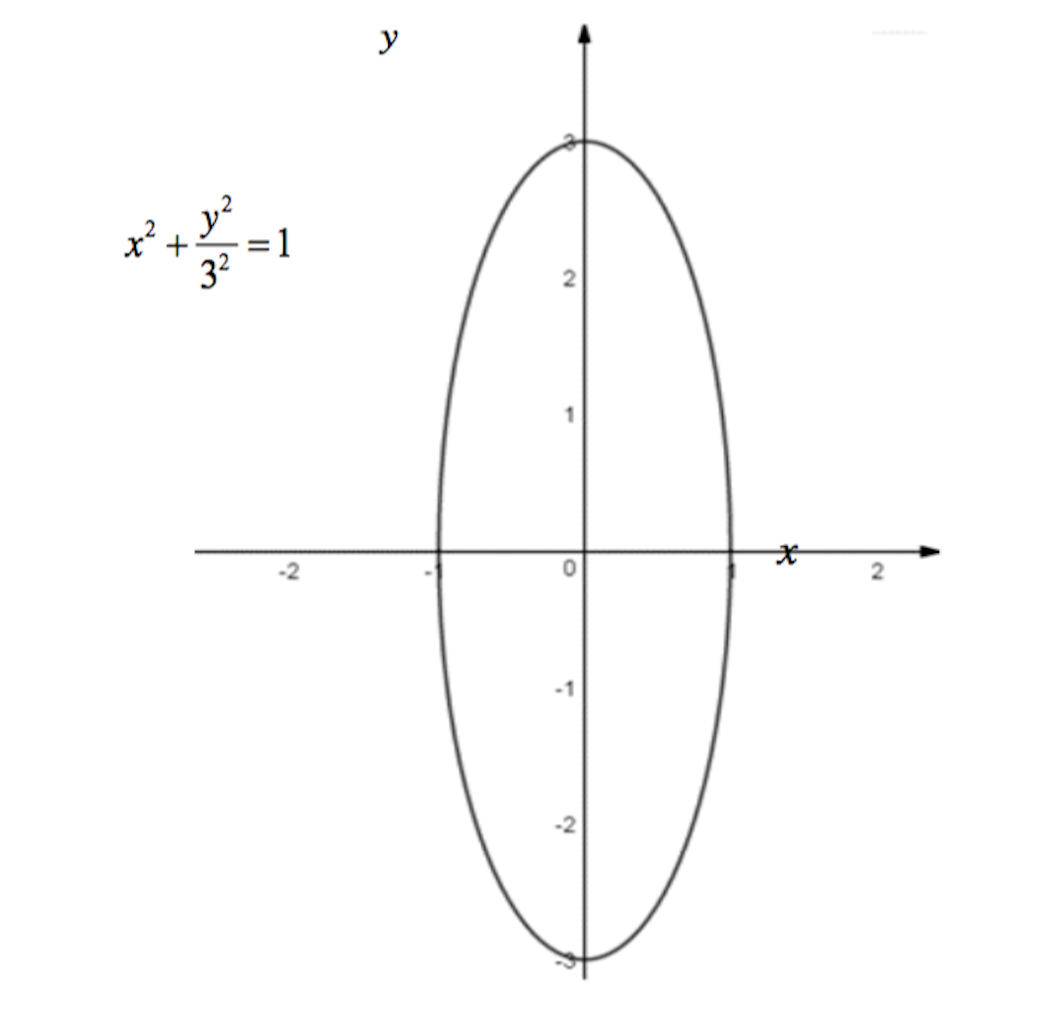
(a)
Firstly, scale by factor ![]() parallel to the y – axis.
parallel to the y – axis.
Secondly, translate by 3 units in the positive x – direction.
Curve D is a circle.
(b)
(i)
(ii)
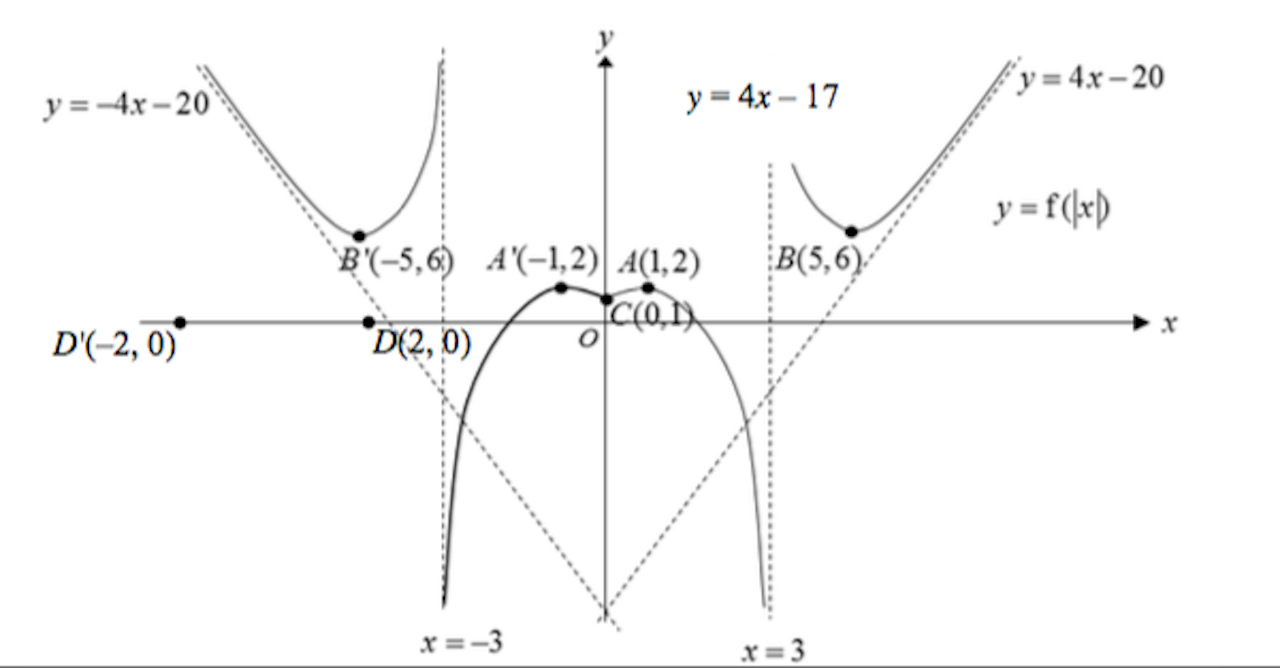
(i)
![]()
![]()
Since ![]()
Using Sine Rule,
![]()
![]()
So y coordinate is given by ![]()
(ii)
Gradient of ![]()
Since QS is always tangential to hump, gradient of ![]()
Since ![]()
![]()
(iii)
Area ![]()
![]() (4dp)
(4dp)
Relevant Materials: MF26