Definite Integral Question #1

This is question that was tested in ACJC H2 Math Prelim P1 2015. A few of my students know how to answer it but were uncertain how to express it.

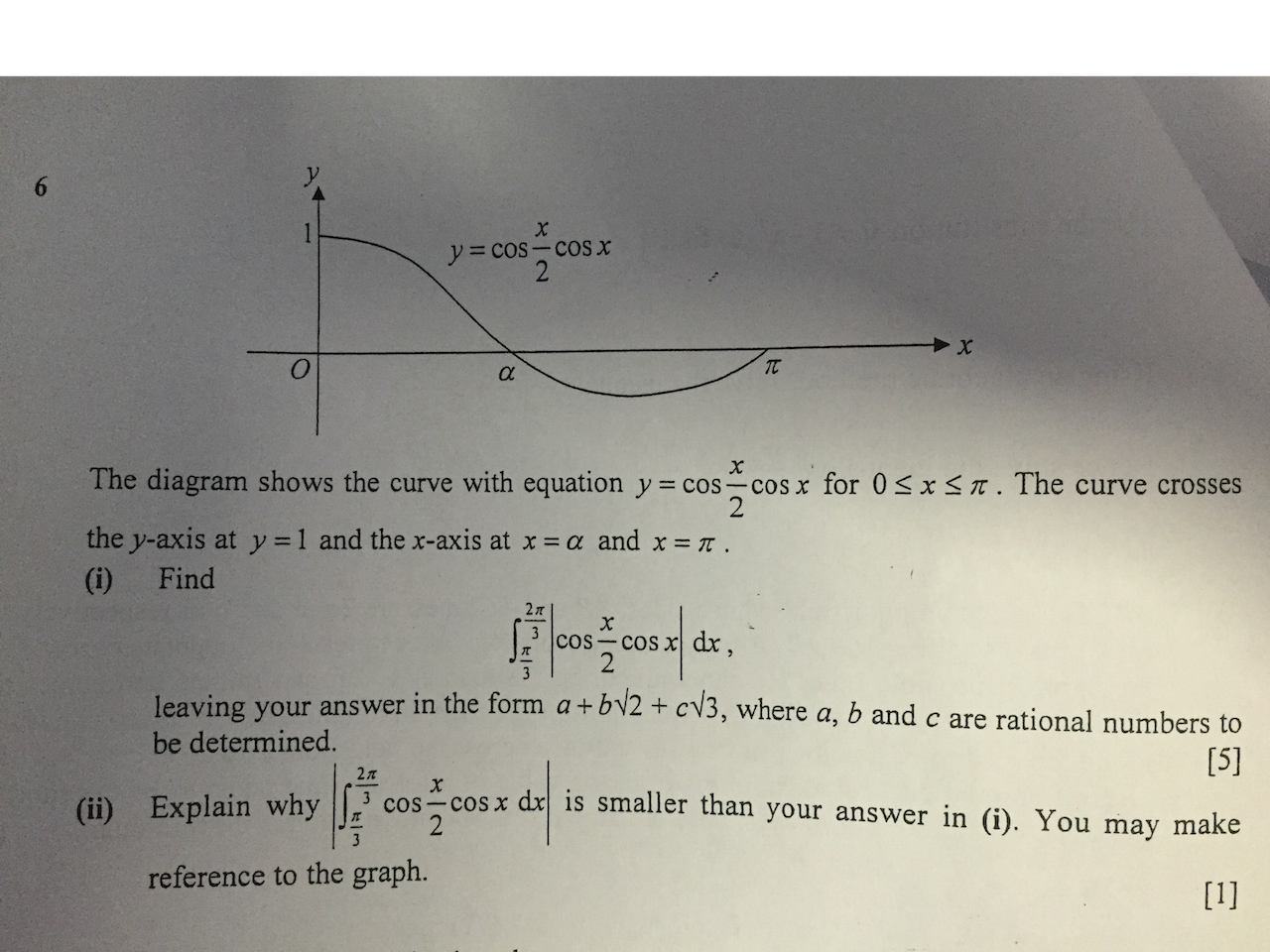
Credits: ACJC Prelims 2015

Most students were concerned with (ii) of the question.

I think the easiest way to prove this, is to first avoid writing too much and attempt to show it mathematically.

$\int_{\pi /3}^{2\pi /3} |cos\frac{x}{2} cosx| dx$
$= \int_{\pi /3}^{pi /2} cos\frac{x}{2} cosx dx - \int_{\pi /2}^{2\pi /3} cos\frac{x}{2} cosx dx$

while

$|\int_{\pi /3}^{2\pi /3} cos\frac{x}{2} cosx dx|$
$= |\int_{\pi /3}^{pi /2} cos\frac{x}{2} cosx dx - \int_{\pi /2}^{2\pi /3} cos\frac{x}{2} cosx dx|$

Thus $|\int_{\pi /3}^{2\pi /3} cos\frac{x}{2} cosx dx|$ will be smaller in magnitude.

Students can also attempt to justify using the area under graph but they must express the answers in words carefully.

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for almost two decades. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Comments

pingbacks / trackbacks

Evaluating Integrals with Modulus | The Culture
[…] may want to reference this recent ACJC Prelim 2015 Question to see if they can do […]
September 16th, 2015 05:00 PM

Cart

Definite Integral Question #1

Leave a Comment
Cancel reply

Definite Integral Question #1

Leave a Comment Cancel reply

Leave a Comment
Cancel reply