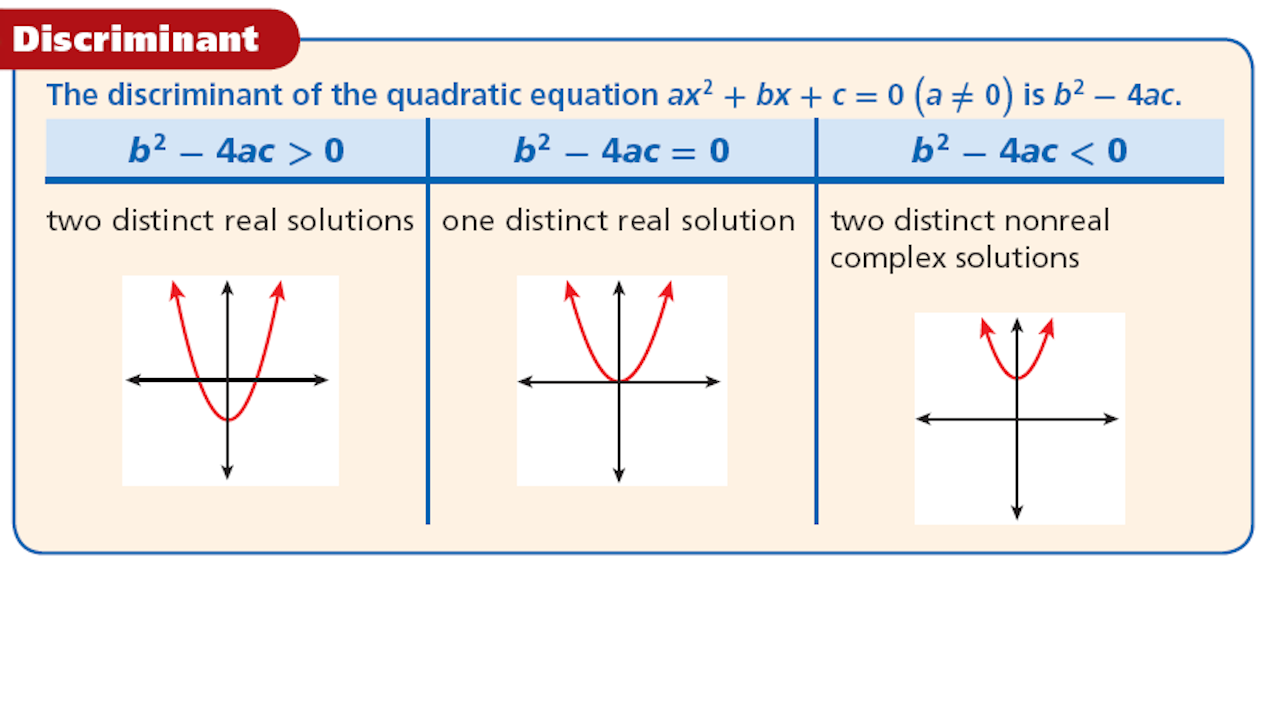
I notice many students forget how discriminant works! I think I should inform A-level students that they need to know how it works and that is one thing they should not return to their O-level teachers. So I thought I share a bit on how to effectively, get it correct and also use it. At the same time, I hope to better the students’ understanding too.
Credits: learn-site.net
Let us first look at the quadratic formula that is well engrained in our heads.
![]()
Now do we see a very familiar formula in there? Yes, its our discriminant formula, ![]() !!! So how does it work, alongside with roots. Let’s look at what a root is next, a root is loosely put, a solution to the equation. I hope it is slowly making sense.
!!! So how does it work, alongside with roots. Let’s look at what a root is next, a root is loosely put, a solution to the equation. I hope it is slowly making sense.
When the discriminant is negative, we have a ![]() which is imaginary, that means we have NO real roots!!
which is imaginary, that means we have NO real roots!!
And when the discriminant is zero, we have ![]() so we only have one single root, that is
so we only have one single root, that is ![]() .
.
BUT if we have a positive discriminant, than due to the ![]() there, we end up with two roots.
there, we end up with two roots.
So I do hope this clears up the air as to how we can relate some algebra with roots. 🙂
This is a question worth looking at from A-levels which test us on discriminant.

[…] An easier approach to remembering discriminant […]
ロレックスブランドコピー
先日購入しました。いろいろ購入前は悩みましたが、ショップレビュー等を見て大丈夫かなと思い購入を決めました。状態もキレイで買って正解でした。梱包も気を使っていただきありがとうございました。また機会があったら是非利用したいお店です!