All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
This is answers for H2 Mathematics (9740). H2 Mathematics (9758), click here.
Numerical Answers (click the questions for workings/explanation)
Question 1: 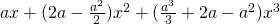 ;
; 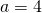
Question 2: 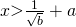 or
or 
Question 3: 2
Question 4: 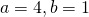 ; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.
; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.
Question 5: 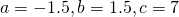 ;
; 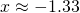 ;
; 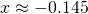 or
or 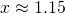
Question 6: 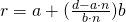
Question 7: 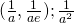
Question 8: 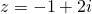 or
or 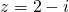 ;
; 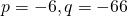 ;
; 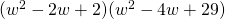
Question 9: 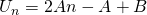 ;
; 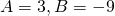 ;
; 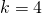 ;
; 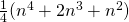 ;
; 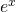
Question 10: 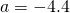 ;
; 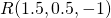 ;
; 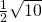
Question 11: 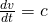 ;
; 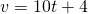 ;
; 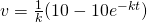
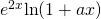
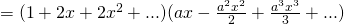
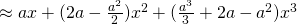
Let 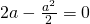
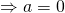 or
or 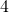
Since  is non-zero,
is non-zero, 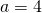 .
.
Let 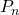 be the preposition “
be the preposition “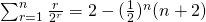 ” for all
” for all 
Let 
LHS 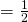
RHS 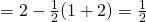
Since LHS = RHS, 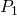 is true.
is true.
Assume 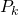 is true for some
is true for some 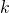 ,
, 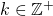
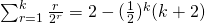
Want to show 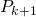 is true
is true
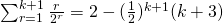
LHS
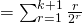
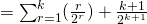
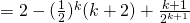
![Rendered by QuickLaTeX.com = 2 - \frac{1}{2^{k+1}} [ 2(k+2) - (k+1)]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-ffff795cc9c4351fef080b8676f03ad2_l3.png)
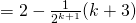
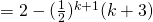
 RHS
RHS
Hence, by Mathematical Induction, since 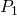 is true,
is true, 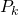 is true
is true 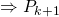 is true,
is true, 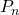 is true for all
is true for all 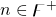
(ii)
As 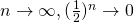
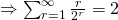
(i)
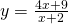
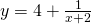
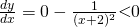 for all
for all 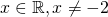
(ii)
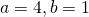
Asymptotes are 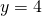 and
and 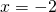
(iii)
First, translate the graph 4 units in negative y-direction.
Then, translate the graph 2 units in positive x-direction.
(i)
Let
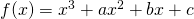
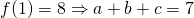 —(1)
—(1)
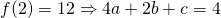 —(2)
—(2)
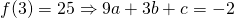 —(3)
—(3)
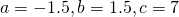
(ii)
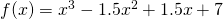
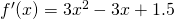
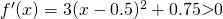
Since 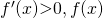 is a strictly increasing function with no stationary point. Thus, it can only have one real root.
is a strictly increasing function with no stationary point. Thus, it can only have one real root.
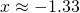
(iii)
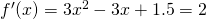
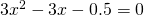
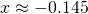 or
or 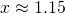
(i)
Set of points lying on the line which passes through a and is parallel to b.
(ii)
Set of points on the plane which has normal vector, n.
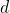 is the displacement of the plane from Origin.
is the displacement of the plane from Origin.
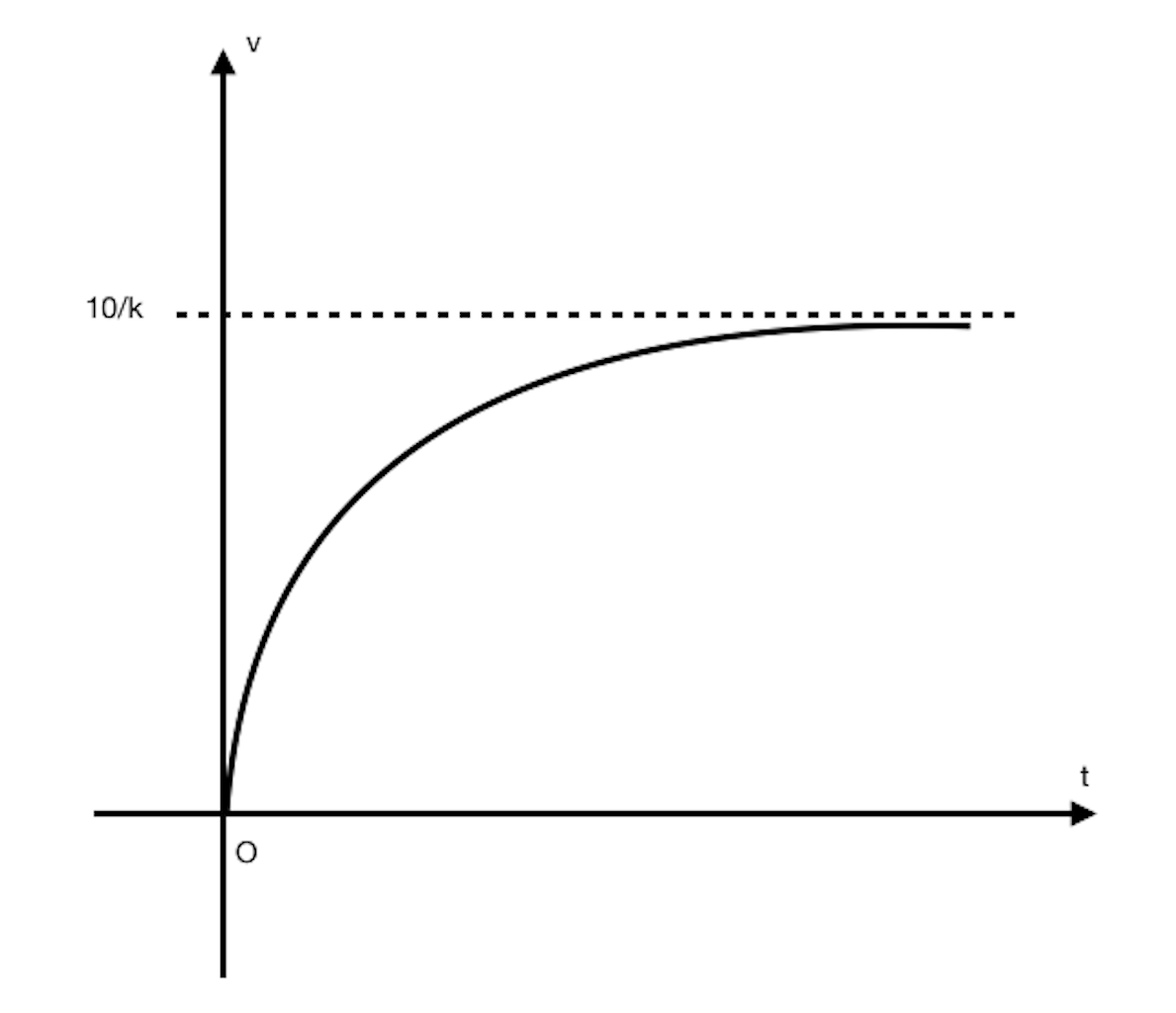
(iii)
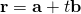
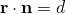
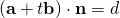
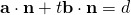
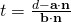
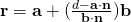
Since 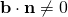 , line is not parallel to plane, the solution represents the point of intersection between the line and plane.
, line is not parallel to plane, the solution represents the point of intersection between the line and plane.
(a)
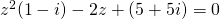
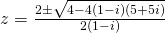
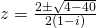
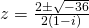
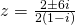
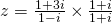
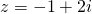
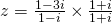
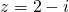
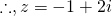 or
or 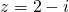
(b)
(i)
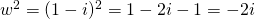
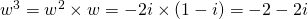
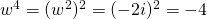
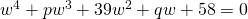
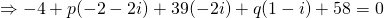
Comparing real and imaginary parts,
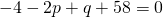
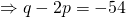 —(1)
—(1)
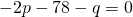
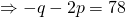 —(2)
—(2)
(1) + (2): 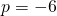
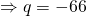
(ii)
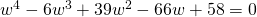
Since all coefficients of 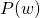 are real,
are real, 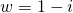 is a root
is a root 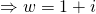 is also a root.
is also a root.
![Rendered by QuickLaTeX.com [w - (1+i)][w-(1-i)] = w^2 - 2w + 2](http://theculture.sg/wp-content/ql-cache/quicklatex.com-eb3f4e70d0ce4bc0e03391bb23444f32_l3.png)
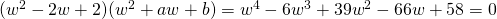
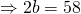
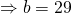
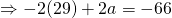
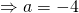
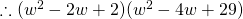
(a)
(i)
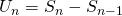
![Rendered by QuickLaTeX.com U_n = An^2 + Bn -[A(n-1)^2 + B(n-1)]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-753663c18d8c7637cccd57794dead32e_l3.png)
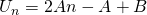
(ii)
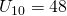
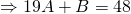 —(1)
—(1)
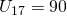
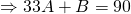 —(2)
—(2)
(2) – (1): 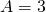
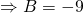
(b)
LHS
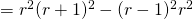
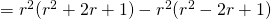
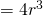
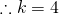
![Rendered by QuickLaTeX.com \sum_{r=1}^n r^3 = \frac{1}{4} \sum_{r=1}^n [r^2(r+1)^2 - (r-1)^2 r^2]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-0bfe15349c894ae89df2cf064acb11a6_l3.png)
Using method of difference,
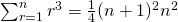
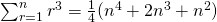
(c)
Let 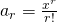
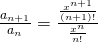
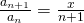
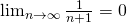
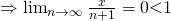
Thus, it converges.
From MF26,
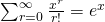
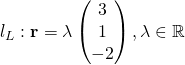
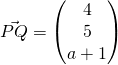
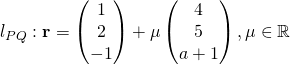
For them to intersect,
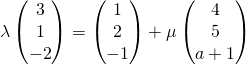 for some
for some 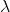 and
and 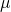
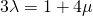 —(1)
—(1)
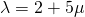 —(2)
—(2)
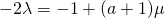 —(3)
—(3)
Solving, 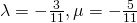
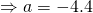
(ii)
Let 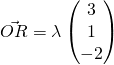 for some
for some 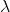
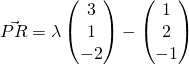
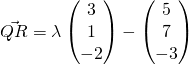
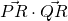
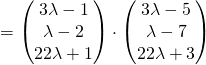
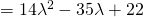
Since discriminant 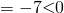
There are no solutions for 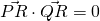
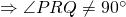
(iii)
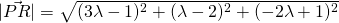
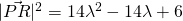
Let 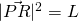
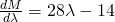
Let 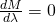
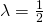
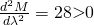
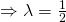 gives minimum
gives minimum 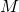 .
.
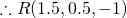
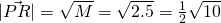 m.
m.
(i)
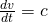
(ii)
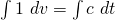
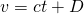 , where
, where 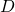 is an arbitrary constant.
is an arbitrary constant.
When 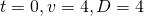
When 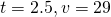 ,
,
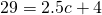
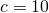
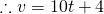
(iii)
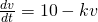
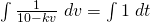
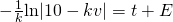 , where
, where 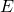 is an arbitrary constant.
is an arbitrary constant.
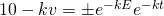
Let 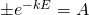
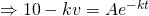
When 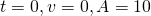 .
.
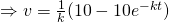
(iv)
As 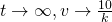 ,
,
Graph of 11(iv)
Relevant materials
MF26
KS Comments
To be honest, this paper is really the same as the H2 Mathematics (9758). They just rephrased everything. You can see for yourself here.
![]() ;
; ![]()
![]() or
or ![]()
![]() ; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.
; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.![]() ;
; ![]() ;
; ![]() or
or ![]()
![]()
![]()
![]() or
or ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()


![Rendered by QuickLaTeX.com = \Bigg[ x \frac{e^{-ax}}{-a} \Bigg]_0^{N} - \int_0^N (1) \frac{e^{-ax}}{-a} ~dx](http://theculture.sg/wp-content/ql-cache/quicklatex.com-14aa7eee149cdb44f9644949e8b6051a_l3.png)
![Rendered by QuickLaTeX.com = N \frac{e^{-aN}}{-a} - \Bigg[ \frac{e^{-ax}}{a^2} \Bigg]_0^{N}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-d59f5818140d1b3e40733aa68b9ffc58_l3.png)
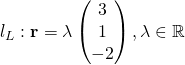
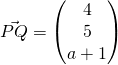
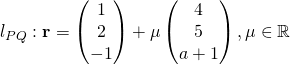
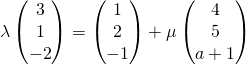 for some
for some 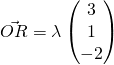 for some
for some 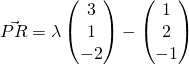
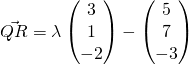
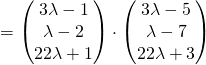


hello there are no answers 🙁
hi for Q10(ii) would it be sufficient to explain that for both P and Q do not lie on line L hence they are both not points of intersection, PRQ will never be 90degrees?
vectors need not intersect to be perpendicular actually.
Hello, got a quick question! For q6(ii) i remembered my teacher specifically saying r.n = d the ‘d’ is simply a constant with no meaning… so shouldnt displacement of plane from origin be d/(n^)?
Thanks!
yes. but n is given to be a unit vector.. it gives a lot of meaning then
Hi, according to the 9740 papers, may I know what are ur thoughts on the expected range of grade to score A grade? Is 70 marks overall for Ppr 1 & 2 guarantee an A?