Today I’ll share a question that came out of CJC Prelim 2017 Paper 1 for H2 Mathematics 9758. I think some of my student would have seen this question before and we discussed it in class before. Very technical question. This is question 11, I’ll share only the first part which is on the application of ratio theorem or mid point theorem. The second part is on application: Ray Tracing which I’ll discuss in class.
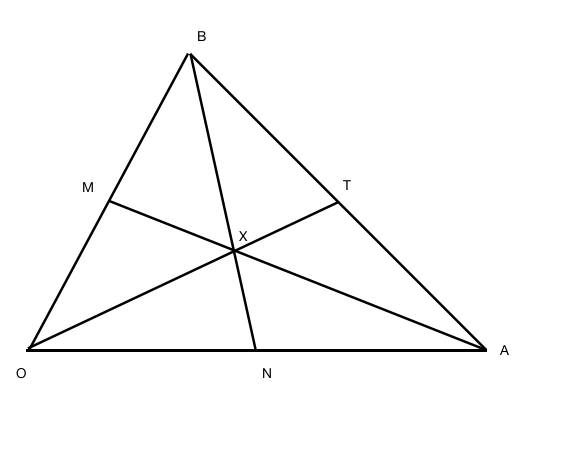
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. For the triangle show below, O, A and B are vertices, where O is the origin. ![]() and
and ![]() . The midpoints of OB, OA and AB are M, N and T respectively.
. The midpoints of OB, OA and AB are M, N and T respectively.
It is given that X is the point of intersection between the medians of triangle OAB from vertices A and B.
(i) Show that ![]()
(ii) Prove that X also lies on OT, the median of triangle OAB from vertex O.