(a)
![]()
![]()
![Rendered by QuickLaTeX.com = \frac{1}{4} [{\begin{pmatrix}1 \\ 1 \\ 2 \end{pmatrix} + \begin{pmatrix}3 \\ 5 \\ 6 \end{pmatrix}}]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-66fdc9a6cb11edc907629f320ca5990a_l3.png)
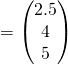
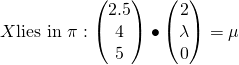
![]()
(b)
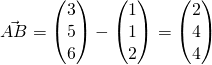
If the plane ![]() contains the line
contains the line ![]() , the
, the ![]() is parallel to
is parallel to ![]() :
:
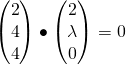
![]()
![]()
![]() and the point
and the point ![]() lies in the plane
lies in the plane ![]() :
:
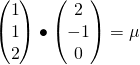
![]()
![]()
Alternatively, you may consider that ![]() :
:
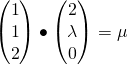
![]() — (1)
— (1)
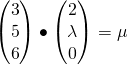
![]() — (2)
— (2)
Solving, ![]()
(a)
![]()
![]()
![Rendered by QuickLaTeX.com = \frac{1}{4} [{\begin{pmatrix}1 \\ 1 \\ 2 \end{pmatrix} + \begin{pmatrix}3 \\ 5 \\ 6 \end{pmatrix}}]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-66fdc9a6cb11edc907629f320ca5990a_l3.png)
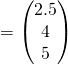
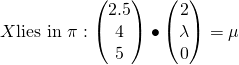
![]()
(b)
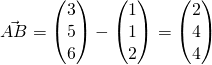
If the plane ![]() contains the line
contains the line ![]() , the
, the ![]() is parallel to
is parallel to ![]() :
:
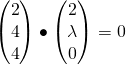
![]()
![]()
![]() and the point
and the point ![]() lies in the plane
lies in the plane ![]() :
:
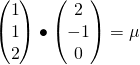
![]()
![]()
Alternatively, you may consider that ![]() :
:
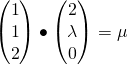
![]() — (1)
— (1)
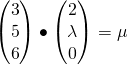
![]() — (2)
— (2)
Solving, ![]()
[…] June Revision Exercise 8 Q6 – The Culture on June Revision Set 8 […]