This page contains all questions and answers asked by students from this class. The most recent questions will be at the top.
Vectors Q7 [Homework]
(i)
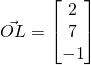
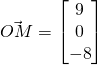
Using ratio theorem, 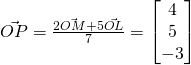
Since ![]() is perpendicular to
is perpendicular to ![]()
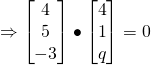
![]()
(ii)
To be a parallelogram, ![]()
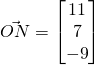
![]()
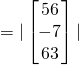
![]()
(iii)
Let 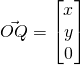
Since ![]()
![]() — (1)
— (1)
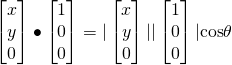 — (2)
— (2)
Solving, ![]()
![]()
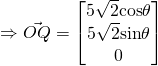
Vectors Q8 [Homework]
(i)
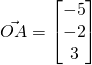
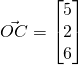
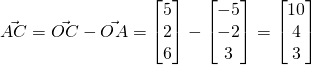
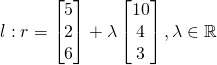
(ii)
Let R be the top of the vertical pillar,
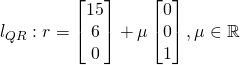
Since R is collinear with A and C, R is the intersection of line AC and QR.
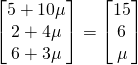
![]()
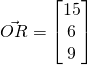 , and the height is 9m.
, and the height is 9m.
(iii)
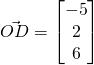
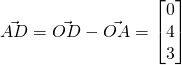
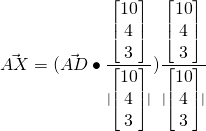
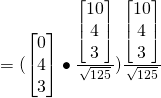
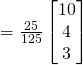
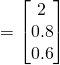
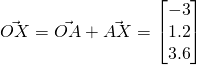
Vectors Q9 [Homework]
(i)
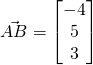
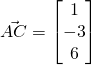
Normal of 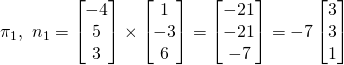
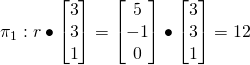
(ii)
Let ![]() be the acute angle
be the acute angle
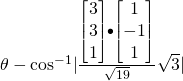
![]()
(iii)
![]() — (1)
— (1)
![]() — (2)
— (2)
Using GC, 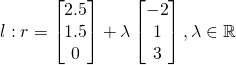
(iv)
Let ![]() be the normal of
be the normal of ![]()
Length of projection ![]()
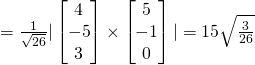
(v)
Required distance ![]()
(vi)
Let normal of 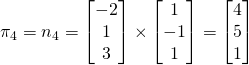
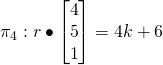
If ![]() intersect at l,n
intersect at l,n![]() lies on
lies on ![]()
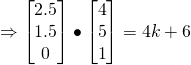
![]()

[…] Math Sat 130pm H2 Math Sat 330pm H2 Math Sun 930am H2 Math Sun 1130am H2 Math Sun 2pm H2 Math Mon 2pm H2 Math Mon 430pm H2 Math Mon 730pm H2 Math Tue […]