So we formally introduced the estimators used in SRS previously. Now, we are interested in how good our estimators are, and if you recall, by good, I refer to accuracy (MSE), Precision (Variance) & Bias (Expectation). Let us look at these qualities of our estimators now.
- Estimator of population mean
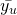
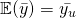 – Unbiased, this implies that
– Unbiased, this implies that 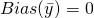
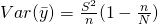 , where
, where 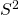 is our population variance.
is our population variance. 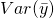 measures the variability among estimates of
measures the variability among estimates of 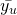 from different samples.
from different samples.
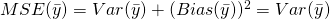 since
since 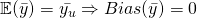 .
. - Estimator of population covariance
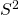
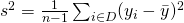 is an unbiased estimator of
is an unbiased estimator of 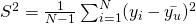
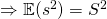 – Unbiased. You should be able to proof this.
– Unbiased. You should be able to proof this.
Since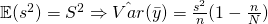 is an unbiased estimator for
is an unbiased estimator for 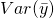
Standard error,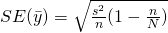
Coefficient of variation,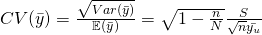
Estimator of Coefficient of variation,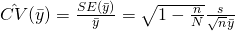
- Estimator of population total t and proportion p
Intuitively, they are both related to the population mean, so estimators should be related to the sample mean.- Lets look at the population total first.
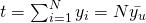
Estimator,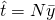
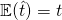 – Unbiased
– Unbiased
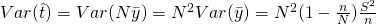
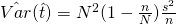
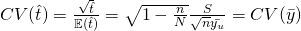
- Next, we look at the population proportion
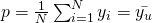
Estimator,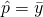
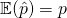 – Unbiased
– Unbiased
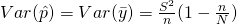
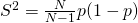
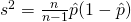
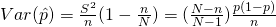
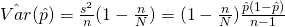
- Lets look at the population total first.
So by now, you should have noticed that this term, ![]() keeps appearing. This is the finite population correction factor (FPC).
keeps appearing. This is the finite population correction factor (FPC). ![]() refers to the sampling fraction that we observe, and the larger the sample size, the larger the sampling fraction, vice versa. Since we assume finite population at the beginning, clearly the largest sample size we can obtain is N, then FPC = 0. This implies that
refers to the sampling fraction that we observe, and the larger the sample size, the larger the sampling fraction, vice versa. Since we assume finite population at the beginning, clearly the largest sample size we can obtain is N, then FPC = 0. This implies that ![]() since we take the one and only possible sample, that is, D = U and
since we take the one and only possible sample, that is, D = U and ![]() . Thus, there should be no variability. On the other hand, if we take samples from extremely large populations, the FPC
. Thus, there should be no variability. On the other hand, if we take samples from extremely large populations, the FPC ![]() . Simply consider taking a sample of size 100 from a population of 100,000 or 100,000,000 units, we have the sample FPC of 0.999 against 0.999999. This effectively gives
. Simply consider taking a sample of size 100 from a population of 100,000 or 100,000,000 units, we have the sample FPC of 0.999 against 0.999999. This effectively gives ![]() . From here, we observe that when dealing with large population, it is the size of the sample, not the percentage of the population sampled, that determines the precision of the estimator. 🙂
. From here, we observe that when dealing with large population, it is the size of the sample, not the percentage of the population sampled, that determines the precision of the estimator. 🙂
To sum things up, we observe how FPC works, and we will see more of it definitely. We can now find our unbiased estimators for population mean, total and proportion. We can also measure the qualities of these estimators. The last take-home message is that since this estimators are unbiased, their qualities which are measured by MSE, is essentially jus the variance. 🙂
Sampling & Survey #1 – Introduction
Sampling & Survey #2 – Simple Probability Samples
Sampling & Survey #3 – Simple Random Sampling
Sampling & Survey #4 – Qualities of estimator in SRS
Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS
Sampling & Survey #6 – Systematic Sampling
Sampling & Survey #7 – Stratified Sampling
Sampling & Survey # 8 – Ratio Estimation
Sampling & Survey # 9 – Regression Estimation
Sampling & Survey #10 – Cluster Sampling
Sampling & Survey #11 – Two – Stage Cluster Sampling
Sampling & Survey #12 – Sampling with unequal probabilities (Part 1)
Sampling & Survey #13 – Sampling with unequal probabilities (Part 2)
Sampling & Survey #14 – Nonresponse
