2015 A-level H1 Mathematics (8864) Paper Suggested Solutions

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

Students are highly encouraged to discuss freely for alternative solutions too.

I typed this, so pardon me if got errors. There should be a handful of errors as I just type and solve as I go. Just refresh as you go along as I’m typing with wifi in a cafe. AND I SKIP A LOT OF STEPS, including denoting my random variables. I’ll get to them probably tomorrow morning.

Question 1

Discriminant
$= b^2 - 4ac$
$= (k-4)^2 -4(-2)(2k)$
$= k^2 -8k + 16 + 16k$
$= k^2 + 8k + 16$
$= (k+4)^2 \ge 0$ for all real values of k.

Thus, there will be at least one real root for all real values of k.

$\Rightarrow$ there exist no real values of k for $2k + (k-4)x - 2x^2$ to be always negative.

Question 2

(i)
$\frac{d}{dx} \frac{3}{(2x-1)^4} = -\frac{24}{(2x-1)^5}$

(ii)
$\int_{\frac{1}{2}}^1 (x+ \frac{2}{x})^2 dx$

$= \int_{\frac{1}{2}}^1 (x^2 + 4 + \frac{4}{x^2})dx$

$= \frac{x^3}{3} + 4x - \frac{4}{x} \biggl|_\frac{1}{2}^1$

$= \frac{151}{24}$

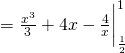
Question 3

(i)
$\frac{dy}{dx} = 12 - 16e^{-2x}$

Let $\frac{dy}{dx}=0 \Rightarrow, x = \frac{1}{2}\mathrm{ln}\frac{4}{3}$

(ii)
$\int_0^a 12x + 8e^{-2x} dx$

$= 6x^2 - 4 e^{-2x} \biggl|_0^a$

$= 6a^2 - 4e^{-2a} + 4$

Question 4

Let H denote the height of big triangle with side y and h denote the height of small triangle with side x.

By Pythagoras’ Theorem, $y^2 = (\frac{1}{2}y)^2 + H^2$

$\Rightarrow H = \frac{\sqrt{3}}{2} y$

Area of big triangle $= 2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}y \times \frac{y}{2} = \frac{\sqrt{3}}{4}y^2$

Perimeter $= 3x + 3(y-2x) = 30$

$\Rightarrow y = 10 + x$

By Pytheagoras’ Theorem, $x^2 = (\frac{1}{2}x)^2 + h^2$

$\Rightarrow h = \frac{\sqrt{3}}{2}x$

Area of small triangle $= 2\times \frac{1}{2} \times \frac{\sqrt{3}{2}}x \times \frac{x}{2} = \frac{\sqrt{3}}{4}x^2$

Required Area $= \frac{\sqrt{3}}{4}y^2 - 3 \times \frac{\sqrt{3}}{4}x^2$

$= \frac{\sqrt{3}}{4}(10+x)^2 - 3 \times \frac{\sqrt{3}}{4}x^2$

$= \frac{\sqrt{3}}{2} [\frac{1}{2}(10+x)^2 - \frac{3x^2}{2}]$

$= \frac{\sqrt{3}}{2} [\frac{1}{2}(100 + 20x + x^2) - \frac{3x^2}{2}]$

$= \frac{\sqrt{3}}{2} (50 + 10x - x^2)$

$\frac{dA}{dx} = \frac{\sqrt{3}}{2}(10-2x) = 0$

$\Rightarrow x = 5$

$\frac{d^2A}{dx^2} = -\sqrt{3} < 0$

Therefore, A is maximum when $x = 5$

$A = \frac{\sqrt{3}}{2}(50 + 50 -25) = \frac{75 \sqrt{3}}{2}$

Question 5

Graph 5i

(ii)
Using GC, $\frac{dy}{dx}\biggl|_{x=0.5} = -1.1567 \approx -1.157$

(iii)
$y - 0.3016416731 = \frac{1}{1.1567}(x-0.5)$

When $x = 0, y = When$ latex y = 0, x =

By Pythagoras’ Theorem, Length $= \sqrt{}$

Question 6

Let X denote the mass of peaches sold by a shop, in grams.

$X \sim N(\mu, \sigma^2)$

$\mathrm{P}(X < 40) = 0.2$

$\frac{40-\mu}{\sigma} = -0.841621 \rightarrow (1)$

$\mathrm{P}(X \le 60) = 0.75$

$\frac{60- \mu}{\sigma} = 0.674489 \rightarrow (2)$

Using GC, $\mu = 51.10237 \approx 51.1$ and $\sigma = 13.19165 \Rightarrow \sigma^2 = 174.01 \approx 174$

Question 7

(i)
Using the ordered list, we pick a random number from 1 to $\frac{1200}{100} = 12$ and then proceed to survey every $12^{th}$ in the list until we have collected 100 names.

(ii)
Due to the periodic and cyclical nature, we might not have a representative sample.

(ii)
Stratified Sampling

Question 8

(i)
$0.42 = p + 2p - 0.03$

$p = 0.15$

(ii)
$\mathrm{P}(A \cup B')$

$= \mathrm{P}(A) + \mathrm{P}(B') - \mathrm{P}(A \cap B')$

$= 0.15 + 0.7 - [\mathrm{P} (A \cup B) - \mathrm{P}(B)]$

$= 0.85 - 0.42 + 0.3$

$= 0.73$

(iii)
$\mathrm{P}(A) \times \mathrm{P}(B') = 0.15 \times 0.7 \ne \mathrm{P}(A \cap B')$

Thus, $A$ and $B'$ are not independent.

Question 9

(i)
Let X denote the number of six Kai obtain out of 8 throws.

$X \sim \mathrm{Bin}(8, \frac{1}{6})$

$\mathrm{P} (X=3) \approx 0.104$

(ii)
$\mathrm{P} (X \le 3) \approx 0.969343$

(iii)
Let Y denote the number of six Lam obtain out of 600 throws.
$Y \sim \mathrm{Bin} (600, \frac{1}{6})$

Since $n = 600$ is large, $np = 100 > 5$ and $n(1-p) = 500 > 5$ ,

$\mathbb{E}(Y)=100$ and $\mathrm{Var}(Y) = \frac{500}{6}$

$Y \sim \mathrm{N}(100, \frac{500}{6})$ approximately

$\mathrm{P}(90 \le Y \le 100)$

$= \mathrm{P} (89.5 \le Y \le 100.5)$ by continuity correction

$\approx 0.397$

Question 10

(i)
Graph to be inserted

(ii)
$r = 0.922441 \approx 0.922$
The r values shows a strong positive linear correlation between the height and weight of the rowing club members.

(iii)
Using GC, $w = 58.0325h -6.3004 \Rightarrow w = 58.0h - 6.30$ (3 SF)

(iv)
Using GC, $w = 90.033 \approx 90kg$

The estimate is reliable since its within data range and the r-value is also close to 1.

Question 11
(i)
Let X and Y denote the masses of Men and Women respective, in kg

$X \sim \mathrm{N}(77, 9.8^2)$

$Y \sim \mathrm{N}(62, 10.6^2)$

$\mathrm{P}(-2 < X - 77 < 2)$

$\mathrm{P}(75 < X < 79)$

$\approx 0.162$
(ii)
Let $Q = X_1 + X_2 + X_3 - (Y_1 + \ldots + Y_4)$

$\mathbb{E}(Q) = -17$

$\mathrm{Var}(Q) = 737.56$

$Q \sim \mathrm{N}(-17, 737.56)$

$\mathrm{P}(Q > 0) \approx 0.266$

(iii)
Let $T = X_1 + X_2 + X_3 + (Y_1 + \ldots + Y_4)$

$\mathbb{E}(T) = 479$

$\mathrm{Var}(T) = 737.56$

$T \sim \mathrm{N}(479, 737.56)$

$\mathrm{P}(T \le 460) \approx 0.242$

Question 12

(i)
To be inserted

(ii)
Required Probability $= \frac{3}{4} \times \frac{2}{5} + \frac{1}{4} \times \frac{3}{4} \times \frac{2}{5} = \frac{3}{8}$

(iii)
Required Probability
$= \mathrm{P}(\mathrm{Student~succeeds~in~qualification~} | \mathrm{~student~fails~Part~I})$

$= \frac{\mathrm{P}(\mathrm{Student~succeeds~in~qualification} \cap \mathrm{student~fails~Part~I})}{\mathrm{P}(\mathrm{student~fails~Part~I})}$

$= \frac{0.25 \times 0.75 \times 0.4}{0.25}$

$= 0.3$

(iv)
Let X denote the number of students out of 5 who passes the qualification.

$X \sim \mathrm{Bin}(5, \frac{3}{8})$

Required Probability $= 1 - \mathrm{P}(X \le 1) \approx 0.61853$

Question 13
(i)
$H_0: \mu = 15.2$

$H_1: \mu \ne 15.2$

Under $H_0, \bar{X} \sim \mathrm{N}(\mu, \frac{2.1^2}{30})$

Test Statistic, $Z = \frac{\bar{X}-\mu}{\frac{\sigma}{n}} \sim \mathrm{N}(0,1)$

We performa a two tailed Z-Test at 5% level significance level.

Using GC, $p =0.06788 > 0.05$

Thus, we do not reject $H_0$ and conclude with insufficient evidence…

(ii)
Unbiased estimate of population mean $= \frac{-32}{40} +18 = 17.2$

$s^2 = \frac{1}{39}(325 - \frac{32^2}{40}) = \frac{499}{65}$

(iii)
An unbiased estimate means the expectations of the estimate is its true population parameter..

(iv)
$H_0: \mu = 18$

$H_1: \mu < 18$

Under $H_0, \bar{X} \sim \mathrm{N}(\mu, \frac{s^2}{30})$

Test Statistic, $Z = \frac{\bar{X}-\mu}{\frac{s}{n}} \sim \mathrm{N}(0,1)$

To reject $H_0, p \le \alpha$

From GC, $p = 0.03391$

$\therefore \{\alpha \in \mathbb{R}| 3.40 < \alpha < 100\}$

Check out Christine’s Comments on the recent GP Essays here too.

Relevant materials

MF15

KS Comments

8864 Answers H1 Mathematics JC MF15 Pure Mathematics Statistics Suggested Solutions Year 2015

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Showing 78 comments

Jiamin November 5, 2015
Reply
Hello, I was just wondering if 75 marks will be enough to hit an A for this year’s H1 paper? Do you feel this year’s paper has been tough? Much thanks!
Student 3 November 5, 2015
Reply
Hi, how many marks will be deducted if did not simplify the answer for 3i? For example is it okay to write 1/2(ln4-ln3) instead of the answer that you gave?
- KS Teng November 5, 2015
  Reply
  its fine. 🙂
  - Jonathan November 7, 2015
    Reply
    Isnt the ans -1/2 ln (3/4) ?
    - KS Teng November 7, 2015
      Reply
      hi, its the same thing. 🙂
      - Jonathan November 7, 2015
        
        Thank you Mr Teng! You really live up to your reputation 🙂 Selfless and always willing to help! I really appreciate it!
qiqing November 5, 2015
Reply
Can’t see the solutions to question 5… like the Pythagoras’ theorem part cut off halfway 🙁
- KS Teng November 5, 2015
  Reply
  Yes, Sorry fixing some of it, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and probably messed up the latex coding.
// November 5, 2015
Reply
Hey, for qn 8(ii), I thought P(A u B’) should be equal to P(B’) + P(A n B’)? as it inclusive of P(A n B)
- KS Teng November 5, 2015
  Reply
  Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
Keith November 5, 2015
Reply
For question 7ii) shouldnt the formula of P(A) + P(B’) – P(AnB’) be used? With P(AnB’) being P(A) – P(AnB).
- Keith November 5, 2015
  Reply
  8ii) sorry
  - KS Teng November 5, 2015
    Reply
    Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
- KS Teng November 5, 2015
  Reply
  Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
// November 5, 2015
Reply
My bad, it should be P(A u B’) = P(B’) + P(A n B’) so the ans would be (1-0.3) + 0.03 = 0.73
- KS Teng November 5, 2015
  Reply
  Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
// November 5, 2015
Reply
My bad, it should be P(A u B’) = P(B’) + P(A n B) so the ans would be (1-0.3) + 0.03 = 0.73
- KS Teng November 5, 2015
  Reply
  Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
Nicholas November 5, 2015
Reply
Question 8ii should be 0.73 🙂
- KS Teng November 5, 2015
  Reply
  Yes, Sorry, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
Clo November 5, 2015
Reply
How many method marks can I get for Q1 if I state discriminant<0 and I expand the equation correctly? (I got the wrong k value though!) Thank you. 🙂
- KS Teng November 5, 2015
  Reply
  yes, definitely. Mine is just one method.
Tan November 5, 2015
Reply
Hi, will the rest of the answers be up soon?
- KS Teng November 5, 2015
  Reply
  Hi, yup. mostly up, except the graphs and tree diagram. haha i need to get home to draw
Stephanie November 5, 2015
Reply
Hi, just wondering what’s the average mark to get an A for this year’s paper? 🙂
Rebecca November 5, 2015
Reply
I think there is an error in qn 2(ii) when you integrated (4/x^2)! but thanks for uploading the solutions to the paper!:)
- KS Teng November 5, 2015
  Reply
  Yes, Sorry changed it, cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and made a handful of careless. Thanks for pointing out!
Student Anon November 5, 2015
Reply
Hi. I believe question 2(ii) has an error as you did not integrate last term properly. I checked using GC too and the answer is 151/24.
Also, can you recheck 8(ii). I got a different answer I think.
- Student Anon November 5, 2015
  Reply
  Ah. Didnt realised you found the error for 8ii already. My bad.
  - Student Anon November 5, 2015
    Reply
    Ah. Also found the 2ii error already. My bad again.
    - KS Teng November 5, 2015
      Reply
      Yup, sorry bout that. I edited it. Thanks for pointing it out. Cos my J1 classes only finished bout 10pm so I kinda want to get it done, and went straight to typing without doing it out. So overlooked the simplest stuffs. :/
  - KS Teng November 5, 2015
    Reply
    no worries. 🙂 Thanks for pointing it out
- KS Teng November 5, 2015
  Reply
  Yup, no worries. Thanks for pointing it out. sorry bout it though cos my JC1 lessons finished at 10pm. haha so i typed all quite choppy and only kinda seeking the lazy man method so overlooked things. Thanks for pointing out!
  - Student Anon November 5, 2015
    Reply
    Hi for final question part (iv) , shouldn’t n be 40? Because it is the second lake sample…
student :) November 6, 2015
Reply
will i be penalised if i went to list the normal distribution for 13(iv) by central limit theorem? i got the distribution values correct though.
also for qn 1, how many method marks do you get for writing down b2-4ac<0 and correct expansion of the equation of the discriminant? (: thanks for uploading the solutions by the way! (:
- KS Teng November 6, 2015
  Reply
  I thought they mentioned its already normal distribution. We can’t approximate to Normal from a Normal through CLT since the condition of CLT states that the distribution must be non-noormal.
  I think if all is fine, you probably lose a mark for missing out on the conclusion
  no worries, I could’ve done better with the solutions had it not been a lack of time on my side.
  - - November 7, 2015
    Reply
    Shucks, I wrote CLT also. But Cambridge practices positive marking right? For 3 marks for 13(iv), if I’m not wrong they award 1m for listing null & alternative hypothesis, 1m for calculating correct p-value and 1m for finding the correct set of values for alpha. So even if the distribution is wrongly list as normal distribution by CLT I’m assuming they will not mark you down/deduct mark for this?
    - KS Teng November 8, 2015
      Reply
      I guess. Since they didn’t have a separate qualitative question that ask that. But I guess if they are practicing positive marking, then its okay haha
daph November 6, 2015
Reply
hi, based on past year experience, do you think 60/100 is enough for a B? 🙂
- KS Teng November 6, 2015
  Reply
  I think you need more than that slightly. I explained a bit on bell curve and you can read more here.
- November 6, 2015
Reply
Hi, how do you think the bell curve will be this year? 🙂
- KS Teng November 6, 2015
  Reply
  Thats a hard questions, and I explained a bit on bell curve and you can read more here.
Student. November 6, 2015
Reply
Hi is there a fixed number of people or percentage for distinctions yearly? Or as long as you score a relatively good A (raw marks), your chances of A will be there? Please advice? Thank you!!!
- KS Teng November 6, 2015
  Reply
  I think there is a percentage of distinctions annually. I explained a bit on bell curve and you can read more here.
Student November 6, 2015
Reply
Hi, I thought 13 should be not rejected instead, because when the p value is greater than the level of significance, it should be accepted and not rejected like you wrote, since there is insufficient evidence at the 5% significance level. Am I right? Thanks.
- KS Teng November 6, 2015
  Reply
  yes haha sorry bout that terrible mistake. Thanks for pointing that out!
Student :) November 6, 2015
Reply
hi there! do you think >85 will be enough to get an A for this paper? do reply! 🙂
- KS Teng November 6, 2015
  Reply
  Definitely 🙂
anon November 6, 2015
Reply
is around 80 sufficient for a distinction? not sure if i’ll get the method marks still if i got the answers wrong…
- KS Teng November 6, 2015
  Reply
  Yup 🙂 Pretty sure 80 is good for A alr.
  - Anon :D November 6, 2015
    Reply
    Are we talking about 80/95 or 80% here? Hahaha
    - KS Teng November 6, 2015
      Reply
      80/95 i hope. :/ we should always be safe haha But i think in general, 80% is really good too.
Hanna November 6, 2015
Reply
Hi, what if we got the correct answer for qn 1 (k< -4), but we didnt write a statement to show that k is always negative…? How many marks will be deducted?
- KS Teng November 6, 2015
  Reply
  i think you might lose a mark for that. then again, they might give you benefit of doubt. haha. it depends on your presentation here. like how you use the discriminant to determine the statement.
Daph November 6, 2015
Reply
Oh okay thanks for the reply! 🙂
Anon November 6, 2015
Reply
For 12(iii) ( 0.25*0.25*0.40)/0.25 = 0.1 right? Why is it 0.3. My answer was 1/3 tho….
- KS Teng November 7, 2015
  Reply
  Yes, sorry, I changed it haha I didn’t really draw the tree as you can see. :/ no time
Shie November 6, 2015
Reply
For 12(iii) it should be (0.25×0.75×0.4)/0.25
- KS Teng November 7, 2015
  Reply
  Great! Thanks for pointing that out. I didn’t really have time to check before putting it up.
Karthigan November 7, 2015
Reply
Thank you for the answers. For the explanation of the unbiased estimate, I said the expected value of the estimator is equal to the corresponding population parameter. Is it correct?
- KS Teng November 7, 2015
  Reply
  yes it is. Its actually more precise than mine haha
  - Anon November 7, 2015
    Reply
    Hi i was wondering if for corr & reg, if i plotted the axises oppositely would i still be awarded marks? Seeing as both variables are random.
    Also for for 13ii, do you know how many marks would be awarded if i only calculated the popn mean without the variance? As the question is 3m. Thanks!! 🙂
    - Ash :) November 7, 2015
      Reply
      Hi your comment regarding the B grade, would you think 63% is enough? Cus that’s what i got i think :/
    - KS Teng November 7, 2015
      Reply
      i think for (i), thats fine. haha but you need to use the appropriate one for the sketch of the line though, along with the calculation of the estimate. Should be 1 if you got the unbiased estimate of the population mean correct.
TJ November 7, 2015
Reply
Hello, thank you for the solution. 🙂 if round off wrongly how many marks do they deduct, is it considered holistically as a script or per mistake made?
and is 72-74/95 can get A?
- KS Teng November 8, 2015
  Reply
  Unlike physics or chem, math is about precision and these will affect your answer marks.
- November 7, 2015
Reply
For 13(iv) is the answer is 3.40 < a 3.40 accepted?
- - November 7, 2015
  Reply
  Sorry, theres a typo. Is the answer 3.40<a 3.40 accepted as a correct answer too?
  - - November 7, 2015
    Reply
    The inequality isnt showing in the comments ah sorry. Is the answer only 3.40 (greater than sign) alpha (smaller than sign) 100?
    Can alpha (greater than sign) 3.40 accepted as a correct answer too?
    - KS Teng November 8, 2015
      Reply
      I think you still must bound it by 100, you can’t test more than 100% after all.
Jonathan November 7, 2015
Reply
Thank you for the answers!
Just checking, do you think 78<Marks<84 over 95 is safe for an A? :/
- KS Teng November 7, 2015
  Reply
  I think it is fine so long as you’re >80%.
Karen November 7, 2015
Reply
Hi sir! Thank you for your answers 🙂 what is your general feel for this paper compared to past years? Do you think 75/100 is sufficient to hit the ‘A’ grade. Thanks!
- KS Teng November 7, 2015
  Reply
  I think that isn’t harder conceptually, like students don’t need to have great knowledge of the syllabus but just have good stamina and be really precise in their work. I think a handful of rounding off errors is made, causing many marks to be lost. :/
  I can’t use the word sufficient here, as it means a lot to someone who studies has been studying Mathematics and Statistics for year. But I can say that > 70/100 is a necessary condition, whereas >85/100 is more than enough. That’s the most I can say. :/
  - Karen November 8, 2015
    Reply
    Haha i agree with your thoughts. Thank you for responding promptly and honestly!
Anon November 9, 2015
Reply
Is 75/95 enough to get an A?
- KS Teng November 9, 2015
  Reply
  sorry, can’t really advise on whats sufficient grade, but it should be ok. 🙂 good luck for the other papers!