2013 A-level H1 Mathematics (8864) Question 5 Suggested Solutions

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
$\mathrm{ln} e^{2-2x} = \mathrm{ln}2 + \mathrm{ln}e^{-x}$
$2 - 2x = \mathrm{ln} 2 - x$
$x = 2 - ln2$

(ii)
$\frac{dy}{dx} = -2 e^{2-2x} + 2 e ^{-x} = 0$
$e^{2-2x} = e^{-x}$
$x = 2$
$y = -e^{-2}$
$\therefore, \mathrm{required~coordinates~is~} (2, -e^{-2})$

(iii)

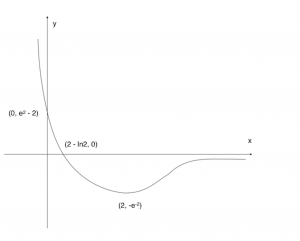
Graph of 5(iii)

(iv)
Area $= \int_0^1 e^{2-2x} - 2e^{-x} dx = 1.93 units^{2}$ using graphing calculator.

KS Comments

Students must show all the requirements of the graph, and please use a GC to check it. Lastly, since (iv) did not require exact answers, we can easily use a GC

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

2013 A-level H1 Mathematics (8864) Question 5 Suggested Solutions

KS Comments

Leave a Comment Cancel reply

Leave a Comment
Cancel reply