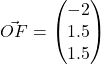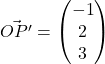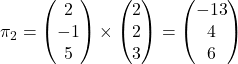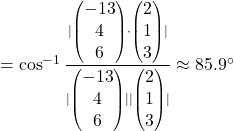Total marks: 5 marks
(a)
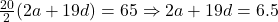
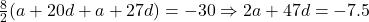
Solving,
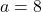
and
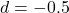
(b)
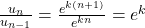
Since
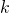
is a constant, then
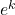
is constant and the ratio is a constant independent of
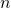
, Thus the sequence is geometric.
Total marks: 7 marks
(a) Observe they are conjugates so
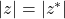
and
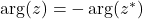
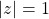
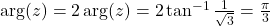
(b)
Point
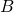
is represented by the complex number
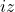
since the length is the same but the argument increased by
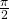
radians.
Total marks: 6 marks
(a)
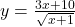
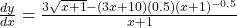
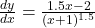
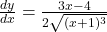
let
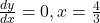
(b)
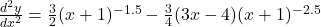
When
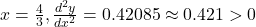
.
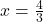
produces a minimum point.
Total marks: 9 marks
(a)
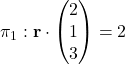
Let the required foot of perpendicular be
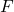
. Then
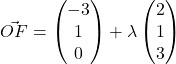
for some
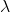
![Rendered by QuickLaTeX.com \bigg[ \begin{pmatrix}-3\\1\\0\end{pmatrix} + \lambda \begin{pmatrix}2\\1\\3\end{pmatrix} \bigg] \cdot \begin{pmatrix}2\\1\\3\end{pmatrix} = 2](http://theculture.sg/wp-content/ql-cache/quicklatex.com-5db598d7e0e1e732f391261e3bf79396_l3.png)
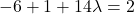
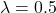
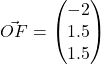
(b)
Let the required reflection of
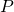
be
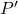
.
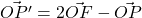
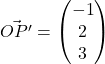
(c)
normal vector of
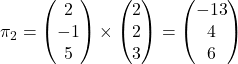
Required angle
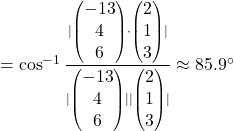
Total marks: 12 marks
(a)
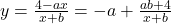
(b)
Firstly, translate the graph

units in the positive
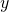
direction.
Secondly, stretch the graph by scale factor of
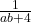
parallel to the
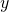
axis.
Lastly, translate the graph
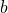
units in the positive
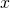
direction.
(c)
Let
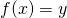
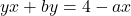
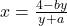
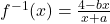
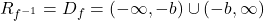
(d)
If
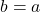
, then
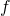
is a self inverse function.
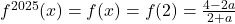
.
Total marks: 14 marks
(a)
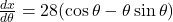
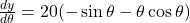
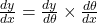
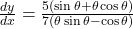
(b)(i)
At C and D,
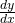
is undefined since tangent is parallel to the
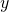
axis.
Let
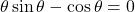
Using GC,
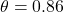
or
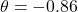
(b)(ii)
Using GC, when
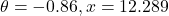
and when
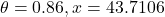
Thus,

(c)(i)
Let
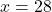
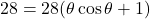
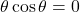
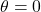
or
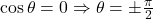
Using GC, we find theta
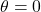
at A.
(c)(ii)
Using GC, we have that
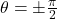
at B
(c)(iii)
Using GC, when
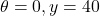
and when
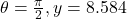
.
Thus,
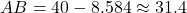
(d)
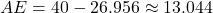
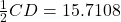
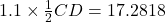
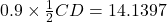
Since
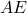
not within the above values, the design does not satisfy the condition.
Total marks: 10 marks
(a)
Since the coefficients of the given polynomial are real and
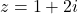
is a root, by conjugate root theorem,
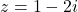
is also a root.
(b)
![Rendered by QuickLaTeX.com [z - (1 - 2i)][z - (1 + 2i)] (z + c) = z^3 + pz^2 + qz - 10](http://theculture.sg/wp-content/ql-cache/quicklatex.com-78c4bd6797245cc522638f3f2adefbe9_l3.png)
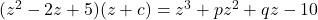
By comparing coefficients of
,
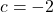
By comparing coefficients of
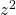
,
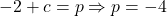
By comparing coefficients of

,
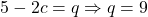
Third root is 2.
(c)
Observe we replace

by
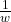
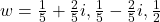
![]()
![]()
![]()
![]() , minimum
, minimum![]()
![]() years
years![]()
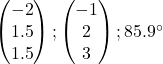
![]()
![]()
![]() , does not satisfy given conditions
, does not satisfy given conditions![]()

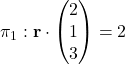
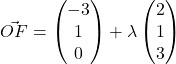 for some
for some ![Rendered by QuickLaTeX.com \bigg[ \begin{pmatrix}-3\\1\\0\end{pmatrix} + \lambda \begin{pmatrix}2\\1\\3\end{pmatrix} \bigg] \cdot \begin{pmatrix}2\\1\\3\end{pmatrix} = 2](http://theculture.sg/wp-content/ql-cache/quicklatex.com-5db598d7e0e1e732f391261e3bf79396_l3.png)