Integrating Trigonometric functions (part 5)

This will be about integrating product of trigonometric functions with no powers involved for example,

$\int sin6xcos21x dx$ or $\int cosxcos5x dx$ .

The simple trick here is to use the product to sum to formulas that can be found here.
For convenience, I’ll insert them here.

So very conveniently,

$\int cosxcos5x dx=\int \frac{1}{2}(cos4x+cosx) dx = \frac{1}{2}(\frac{sin4x}{4}+sinx)$ .
Now you see the usefulness of the product to sum formula! Better learn how to find them!

For trigonometric functions with powers involved, you can refer to part 1 to part 5.

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Showing 2 comments

pingbacks / trackbacks

Trigonometric related articles – The Culture
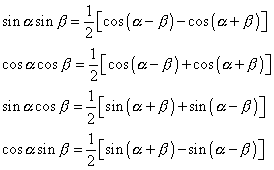
[…] (2) 4. Integrating Trigonometric Functions (3) 5. Integrating Trigonometric Functions (4) 6. Integrating Trigonometric Functions (5) 7. Easiest way to remember cosec, sec, and cot […]
April 18th, 2016 04:18 PM
Integration related articles – The Culture
[…] (2) 3. Integrating Trigonometric Functions (3) 4. Integrating Trigonometric Functions (4) 5. Integrating Trigonometric Functions (5) 6. Leibniz’s Formula for 7. Simpson’s Rule 8. Evaluating Integrals with […]
April 20th, 2016 04:11 PM

Cart

Integrating Trigonometric functions (part 5)

Leave a Comment
Cancel reply

Integrating Trigonometric functions (part 5)

Leave a Comment Cancel reply

Leave a Comment
Cancel reply