All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1: ![]()
Question 2: ![]()
Question 3: ![]()
Question 4: ![]() ; away from the starting point
; away from the starting point
Question 5: ![]()
Question 6: ![]()
Question 7: ![]()
Question 8: ![]()
Question 9: ![]()
Question 10: ![]()
Question 11: ![]()
Note to students: You can and should be using GC here.
![]()
![]()
By comparing coefficients of real and imaginary parts, ![]()
![]()
Using GC, other roots are ![]() and
and ![]() .
.
(a) ![]()

From the graph, we can observe that each rectangle has a constant width of ![]() and the height of each rectangle is given by the
and the height of each rectangle is given by the ![]() coordinate. Also note that the same of rectangles here is an underestimation of the area under the curve
coordinate. Also note that the same of rectangles here is an underestimation of the area under the curve ![]() from
from ![]() to
to ![]() .
.
Sum of rectangles ![]()
Sum of rectangles ![]()
Sum of rectangles ![]()
Actual area under the graph ![]()
Thus, ![]()
(b)
Required expression: ![]()
Explanation (if you are interested): The rectangles in (a) touches the curve on the left corners while the rectangles in (b) is meant to touch the curve on the right corners. Thus, we simply need to “shift” one term to the right.
(c)![]() and
and ![]()
![]()
![]()
![]() using GC.
using GC.![]()
![]()
![]() using GC.
using GC.![]()
(d)
Let ![]() .
.

Note: There are many possible answers here, a decreasing function should be good. My choice came up to me as the easiest. I will verify it.![]()
![]()
(a)(i)![]()
(a)(ii)![]()
![]() using the GC.
using the GC.
(b)(i)
Consider ![]() , then f is not defined when
, then f is not defined when ![]() since
since ![]() is a vertical asymptote. Thus,
is a vertical asymptote. Thus, ![]() .
.
(b)(ii) For functions to be self-inverse, we need both functions to have the same rule, domain and range. Observe that ![]() has a horizontal asymptote at
has a horizontal asymptote at ![]() . Then
. Then ![]() .
.
Observe that ![]() , however the function will not be a 1-1 function if f is a horizontal line, thus
, however the function will not be a 1-1 function if f is a horizontal line, thus ![]() .
. ![]() and
and ![]()
(b)(iii) Since we have that it is self-inverse, then ![]() .
.![]()
(a)
Total time ![]()
(b)
Total distance ![]()
Total time ![]()
Average speed ![]()
(c)
Consider ![]() , this implies that Suzie is on her 17th lap. Thus she is swimming away from her starting point.
, this implies that Suzie is on her 17th lap. Thus she is swimming away from her starting point.
(a)![]()
![]()
![]()
(b)![]()
![]()
![]()
![]()
(c)![]()
![]()
![]() since
since ![]()
![]()
(d)![]()
![]()
![]()
![]()
![]()
![]()
Let ![]() be the score of the spinner.
be the score of the spinner.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Using GC, ![]() .
. ![]()
Mean score ![]()
(a) Number of ways ![]()
(b) Number of ways ![]()
(c) Required probability ![]()
(a) Manager should carry out a 1-tail test since he wishes to test if the population mean life span is greater than 20 000 miles.
Let ![]() be the population mean life span of tyres.
be the population mean life span of tyres.
Let ![]() be the null hypothesis.
be the null hypothesis.
Let ![]() be the alternative hypothesis.
be the alternative hypothesis.
Test ![]()
against ![]()
(b)
Unbiased estimates of population mean ![]() miles
miles
Unbiased estimates of population variance ![]()
Note that if you did not multiply, i.e., did in thousand miles. It is perfectly fine, but you should note to state the ![]() instead, in order to be coherent for the
instead, in order to be coherent for the ![]() value.
value.
(c)
Under ![]() , since
, since ![]() is sufficiently large, by central limit theorem,
is sufficiently large, by central limit theorem,![]() approximately.
approximately.![]()
Since ![]() , we do not reject
, we do not reject ![]() at 5% significance level and conclude with insufficient evidence that the mean life span of the tyre is more than 20000 miles.
at 5% significance level and conclude with insufficient evidence that the mean life span of the tyre is more than 20000 miles.
(d)
As the distribution of the tyre is unknown initially, we will need to take a sufficiently large sample size that is greater than 30 in order to approximate the sample mean life span to a normal distribution by central limit theorem. Thus a sample size of 15 will be inappropriate.
(a)
The given product moment correlation coefficient suggests a strong positive linear correlation between the bivariate data. The given scatter diagram also suggest that as ![]() increases,
increases, ![]() increases increasingly and at the start,
increases increasingly and at the start, ![]() was increasing slower. Thus a linear model will not provide a good model.
was increasing slower. Thus a linear model will not provide a good model.
(b)(i)
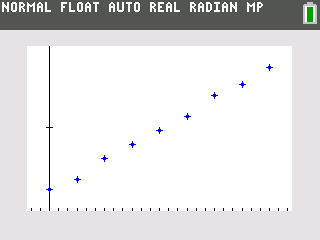
(b)(ii)
Using GC, ![]()
(c)
Both models suggest that there is a strong positive linear correlation between the bivariate data. However, the product moment correlation coefficient for model in (b) is closer to 1 and suggests a stronger linear correlation as compared to that for model in (a). Based on the given scatter diagram, as time passes, the mass should increase increasingly and thus model (B) is more appropriate.
(a) Let ![]() be the mass of the seat, in kg.
be the mass of the seat, in kg. ![]()
![]()
![]()
Using GC, ![]() and
and ![]()
(b) Let ![]() be the mass of the legs, in kg.
be the mass of the legs, in kg. ![]()
![]()
(c) Let ![]()
![]()
![]()
![]()
![]()
(d) Let ![]()
![]()
![]()
![]()
![]()
(e) Let ![]() and
and ![]() be the diameters of the holes in the seats and diameters of the holes of the legs, respectively, in mm.
be the diameters of the holes in the seats and diameters of the holes of the legs, respectively, in mm.![]()
![]()
![]()
![]()
(a)(i) The light fittings should be selected such that he obtains a random sample, i.e., each light fitting has an equal chance of being selected, independently of each other.
(a)(ii) There are several ways to solve this, the best would be to use the GC and calculate using the frequency functions. The probability here is akin to proportion of light fitting that is faulty out of the 150 days of 100 samples each day. So ![]() .
.
(a)(iii)
![]()
Note that expected number need not be a whole number.
(b)(i) The event that the heating elements for electric ovens is found to be faulty is independent of another heating elements for electric ovens. The probability that heating elements for electric ovens is found to be faulty is constant thoughout the sample.
(b)(ii) ![]()
![]()
![]()
(b)(iii)![]()
Let ![]() be the number of days with more than 3 elements found to be faulty, out of 5 days.
be the number of days with more than 3 elements found to be faulty, out of 5 days.![]()
![]()
(b)(iv)
Let ![]() be the number of faulty elements found, out of 400 elements.
be the number of faulty elements found, out of 400 elements.![]()
![]()
[…] 2021 A-level H2 Mathematics (9758) Paper 2 […]
Leave a CommentCancel reply



Wasn’t 8 in thousand miles?
Yes, Both are ok, it really depends on what your is based on, depends on whether you used
is based on, depends on whether you used 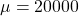 or
or 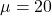 .
.
hi for qn 2, what’s the rewritten equation, the one that shows area larger than A? the one mark qn
Hi, yes, the equation is there. As for other parts, I’ll add it in now. Sorry, due to some issues and complaints, I can’t post so fast.
hi for qn 8, i used everything in terms of thousand miles, except the first part where i put my hypothesis as 20000. but for part c i changed it to 20. is it ok to do so or if no, how many makrs will i lose?
Bro I did the same thing. I think as long as you stated that u use in thousand miles its fine. And if u got the same p value it should be fine.
I agree with you both. so long as units stated, its ok. The p value will not be affected. But you will should adjust your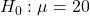 to be coherent.
to be coherent.
i wrote thousand miles for part b but just wrote the new hypothesis as 20, its ok?
What if I used Ho:Miu=20 for the first part but I didn’t specify that it’s in thousand miles? Will I lose all 3 marks? I wanted to be coherent with the later parts of the question.
How much do you think an A would be? I got about 76%-79%, is that enough?
Hi, I can’t comment much. In my humble opinion, I believe you did well and definitely deserve the A. 🙂
is it accepted if we took the average of the 3 speeds (speed for each of the 10 lengths) and got 1.19 (3sf) instead of taking total distance over time i interpreted it as average of the 3 speeds
Average speed is total distance divided by total time taken. This is a formulae that is taught in kinematics in secondary school.
how many marks out of 5 do you think would be given to find the average speed (1 or 2 marks)
total distance – 1 mark
total time – 1 mark
use of GP correctly – 1 mark
average speed – 1 mark
answer – 1 mark
just my opinions.
also for question 10 instead of using sigma=0.0799 which is the 3sf version given in the question what if we used the more accurate value for sigma like the 5sf version for the rest of the question will the answer be accepted.
also for the inappropriateness of 15 question: what if we just said a large sample for example 50 is required for the sample mean lifespan of the tyres to approximately follow a normal distribution by CLT instead of saying sample size of 15 is too small for the sample mean to approximately follow a normal distribution
Hi, for exam purposes, we are supposed to use “shown” values for subsequent calculations and not 3 s.f. In this case, the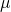 should be minimally 5 s.f. while
should be minimally 5 s.f. while 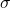 since its shown to be 0.0799, we should use this.
since its shown to be 0.0799, we should use this.
The general sufficiently large size for CLT is 30 now, and it is standardised throughout the JCs.
how many marks would they deduct if we didnt use the shown value for sigma and used the 5sf value instead
if it doesn’t affect the final answer, then it won’t bite. else, you probably lose answer marks only. since all the methods are accurate.
What is the answer to the last part of Q2? Is it a downward sloping curve?
Possible typo in your answer to Q4c: 17th lap or 7th lap?
Hi, yes, I’ll add it in the graph. Sorry, due to some issues and complaints, I can’t post so fast.
Re Q4, 17th lap overall, 7th lap of the constant sequence. Same conclusions. 🙂
As for the graphs, there are many answers.
hello mr teng!! how would u rate this year’s paper!!
I feel that its fairly ok compared to that of 2020 and 2019. The setter has made good efforts to guide students. Can be seen from “integration by parts twice” and using values from (a), etc. Good normal of show questions and certain questions could be verified with GC. The whole paper is healthily guided, a student who is confident to try will generally make good progress through the paper.
This is my personal comment.
Hi do stats have ecf like if I wrote the distribution wrongly but the steps to obtain is okay would I still get the method marks
Hi, I take it that “okay” refers to the correct method, but the distribution is wrong and answer is wrong. You should be able to get 1 mark if its a 3 mark question. For instance, being able to express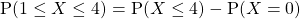 should give you 1 mark, should the question be 3 marks, since 1 mark is lost for the answer, and 1 mark for the distribution. So it really depends on how many marks is allocated. 🙂
should give you 1 mark, should the question be 3 marks, since 1 mark is lost for the answer, and 1 mark for the distribution. So it really depends on how many marks is allocated. 🙂
For question 9c, a ln x on t model means the mass, x, increases increasingly rather than decreasingly
Hi Kelvin, thank you for pointing it out. Amended. Much appreciated. 🙂