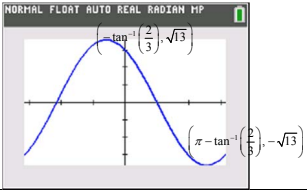
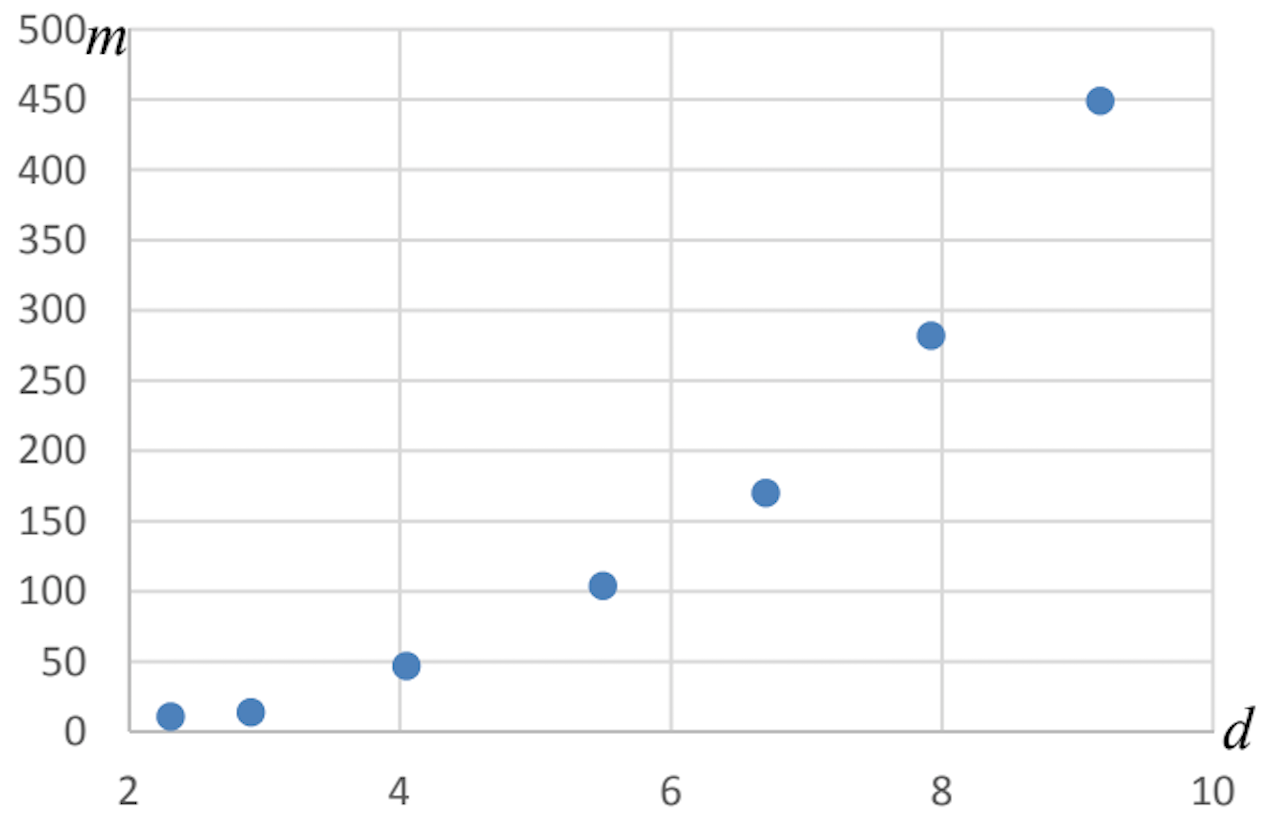
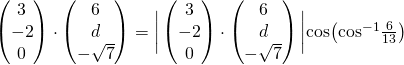All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
Numerical Answers (click the questions for workings/explanation)
Question 1: ![]()
Question 2: ![]()
Question 3: ![]()
Question 4: ![]()
Question 5: ![]()
Question 6: ![]()
Question 7: ![]()
Question 8: ![]()
Question 9: ![]()
Question 10: ![]()
Relevant materials
KS Comments
The specimen paper 2 was useful to provide us with a glimpse of what is to be expected of the upcoming syllabus. The DRV question and binomial question briefly showed us that we need to explore more applications of statistics. It is definitely different from the old 9740 H2 Mathematics Syllabus as the questions are more intuitive and seek to push students’ imaginations more.
In this paper, Question 9 and Question 10 strive to be the application questions in real world context. On the other hand, Question 6 and Question 7 require students to understand/ justify the appropriateness and suitability of models.