All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
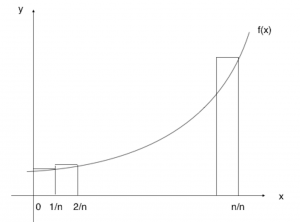
(i)
Width of each rectangle ![]()
Total area of rectangles ![]()
When ![]() , we have the exact area instead.
, we have the exact area instead.
![]()
(ii)
![]()
![]() where
where ![]()
![]()
![]()
![]()
Back to 2015 A-level H2 Mathematics (9740) Paper 1 Suggested Solutions
KS Comments:
(i) needs some explanations to be done and there are many ways to present it, just make sure you use a graph. They are looking for students to be able to write out the definition of integration here. This question should be one of those “high A” questions to set students apart. You don’t have to use summation signs here too. (ii), we can check answer with GC.


[…] Question 3 Question 3 […]
[…] question was sent in by a student, which I think is rather interesting given 2015 A’levels P1 Q3 had something […]
[…] Problems (Click to link to the solutions) N2016/P1/Q3 N2016/P1/Q8 N2016/P1/Q10(a) N2015/P1/Q3 […]
[…] P1: 3, […]