2011 A-level H2 Mathematics (9740) Paper 1 Question 8 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
\int \frac{1}{100-v^2}dv = \frac{1}{20} \mathrm{ln}|\frac{10+v}{10-v}| + C

(ii)
(a)
\frac{dv}{dt} = 10 - 0.1 v^2

\int \frac{1}{100-v^2} dv = \int \frac{1}{10} dt

\frac{1}{20} \mathrm{ln} |\frac{10+v}{10-v}| = \frac{1}{10} t + C

When t = 0, v = 0 \Rightarrow c = 0

\therefore t = 0.5 \mathrm{ln} |\frac{10+v}{10-v}|

When v = 5, t = 0.5\mathrm{ln}3

(b)
When t = 1

\Rightarrow 2 = \mathrm{ln}|\frac{10+v}{10-v}|

\pm e^2 = \frac{10 + v}{10 - v} Reject - e^2 since v = 0 when t = 0

e^2 (10 - v) = 10 + v

10 e^2 - 10 = v - e^2v

v = 7.62

(c)

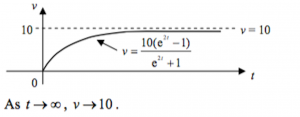
Graph of 8(b)

Graph of 8(b)

From the graph, As t \rightarrow \infty, v \rightarrow 10

KS Comments:

(i) can be resolved easily with the MF15 formula.
(ii), students can actually plot the entire graph of t against v into the graphing calculator and calculate the v when t = 1. They should draw the graph out then. Should they do this, (c) will be solved conveniently.

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    2011 A-level H2 Mathematics (9740) Paper 1 Question 5 Suggested SolutionsJC Mathematics
    Summation Question #3JC Mathematics