All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions
Numerical Answers (workings/explanations are after the numerical answers. Click to expand.)
Question 1: ![]()
Question 2:
Question 3: ![]()
Question 4: ![]() or
or ![]() ;
; ![]()
Question 5: ![]()
Question 6: ![]()
Question 7: ![]()
Question 8: ![]()
Question 9: ![]()
Question 10: ![]()
Question 11: ![]()
Question 12: ![]() ; cannot see since
; cannot see since ![]() ;
; ![]() ; no
; no
Total marks: 4 marks
Since
At
At
Using GC,
Note: Students can verify this answer by plotting the graph.
Total marks: 3 marks
Since ![]() is a unit vector, then
is a unit vector, then ![]() .
.
Since ![]() , then
, then ![]()
![]()
![]() , where
, where ![]() is the angle between
is the angle between ![]() and
and ![]()
![]()
![]()
Thus, ![]() and
and ![]() are perpendicular to each other.
are perpendicular to each other.
Total marks: 4 marks
(a) For ![]() to be a root, we must be able to apply conjugate root theorem. Thus, all coefficients of the polynomial should be real numbers. We have that
to be a root, we must be able to apply conjugate root theorem. Thus, all coefficients of the polynomial should be real numbers. We have that ![]() .
.
(b) ![]()
![]()
![]()
Thus, ![]()
Note: Students can verify this answer by using the GC’s polynomial root finder function
Total marks: 6 marks
(a)![]()
![]()
![]()
![]()
![]()
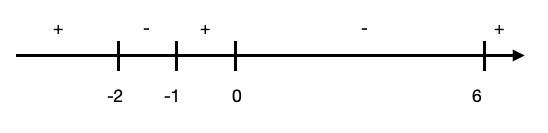
![]() or
or ![]()
(b)
Replace ![]() by
by ![]()
![]() (rejected,
(rejected, ![]() or
or ![]()
![]()
Note: Students can verify this answer by plotting the graph.
Total marks: 7 marks
(a) ![]()
![]()
![]()
![]()
![]()
![]()
(b) Using GC, since ![]() ,
, ![]() and
and ![]()
(c) Note that ![]() is a GP with first term
is a GP with first term ![]() and common ratio
and common ratio ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
Total marks: 8 marks
(a) ![]()
![]()
When ![]()
Tangent at ![]() is given by
is given by ![]()
![]()
![]()
Thus, ![]()
(b) Since the tangent cuts the origin, then![]()
(c)
Required area![]() , using GC.
, using GC.
Total marks: 8 marks
(a)![]()
![]()
![]()
![]()
![]()
(b) Note: there are some issues with the rendering here, you should do method of difference.![]()
![]()
![]()
![]()
![]()
![]()
![]()
(c)![]()
![]()
![]()
![]()
![]()
Observe that ![]() .
.
Thus, the possible values are ![]()
Note: Students can verify this answer by calculating the sigma with the GC.
Total marks: 9 marks
(a) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, ![]()
(b)![]()
When ![]()
Thus, ![]()
Note: we can verify the answers using standard series in exam.![]()
![]()
![]()
![]()
(c) ![]()
![]()
![]()
By comparing, ![]() and
and ![]() .
.
Total marks: 10 marks
(a)![]()
![]()
![]() , and
, and ![]()
(b)
Let ![]() , then
, then ![]()
![]()
Thus, coordinates are ![]() .
.
(c) Observe that when ![]()
![]()
![]()
![]()
![]()
![]()
Total marks: 14 marks
(a) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(b) The axial intercepts are ![]() , and the asymptotes are
, and the asymptotes are ![]() and
and ![]() .
.
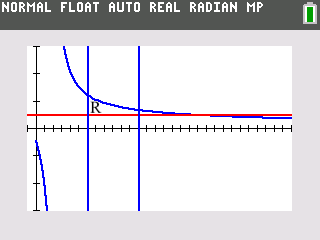
(c)![]()
![]()
![]()
![]()
![]()
![]()
Thus, ![]()
(d)![]() using GC.
using GC.
Total marks: 12 marks
(a)(i)![]()
Thus, ![]()
(a)(ii) We have that ![]()
(b)![]()
![]()
![]()
![]()
![]()
![]() , where
, where ![]()
Let ![]()
![]()
![]()
Thus, ![]() and
and ![]()
(c)![]()
![]()
![]()
When ![]()
Let ![]() , using GC,
, using GC, ![]() seconds
seconds
Total marks: 15 marks
(a) Let ![]() be the points nearest to the controller and let
be the points nearest to the controller and let ![]() be the controller.
be the controller.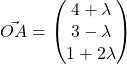 for some
for some ![]()
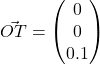
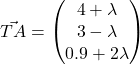
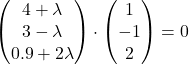
![]()
Thus, the coordinates of ![]() is
is ![]() .
.
(b) 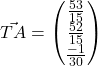
![]()
Thus, the controller will not be able to see.
(c) (i) Clearly, the paths are not parallel. Now suppose the path intersect, then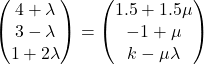
We have that ![]()
![]()
Solving, ![]() and
and ![]() . Thus
. Thus ![]() .
.
Thus, ![]()
(c) (ii)
Required angle 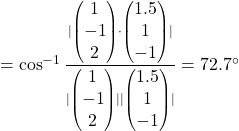
(d) (i)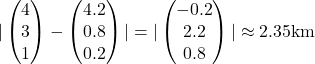
(d) (ii)
For the distance to be the shortest, the resultant vector 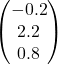 should be perpendicular to both the paths.
should be perpendicular to both the paths.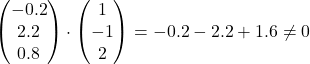
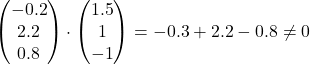
Since the resultant vector is not perpendicular to both the paths, the distance found is not the shortest.

Hi, for 11(b) B should be -2 if I remember correctly? Because in the question, exponent for e^Bt had no negative sign in front of the B.
I also need to verify if Q9(c) definite integral range is from 0 to Q or P to Q. Because I may have misread the question during the paper but I did from P to Q.
I’m not sure if you have access to the paper exactly as it is, in that case, my information could be wrong.
Hello, actually I can’t recall whether they had a negative sign in from of the exponent too. For 9c, I think it was 0 to Q, but I may have recalled wrongly too.
Hello, for qn 6 (c), was the answer supposed to be in 1dp/2sf? I recall giving mine to 3sf as 5.40
hello. its to 1 decimal places.