All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions. Sorry, due to copyrights issues, I cannot share the paper.
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1: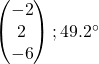 
Question 2: 
Question 3: 
Question 4: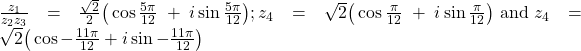 
Question 5: 
; refer to solutions below for explanation.
Question 6: 
Question 7: 
Question 8: 
Question 9: 
Question 10: 
Question 11: 
(i) [Maximum marks: 2]
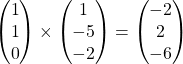
(ii) [Maximum marks: 2]
Required angle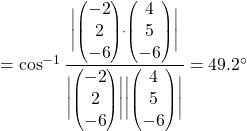 
Note/ Comment: For (i), if students simplified, it is ok since the questions simply asked for a vector normal to the plane.
Differentiating with respect to 
,
Let 
, where
Note/ Comment: Slightly tedious but fully manageable. A more elegant approach will be to consider
and differentiate from here.
(i) [Maximum marks: 3]
(ii) [Maximum marks: 4]
Note/ Comment: Quite a standard question. Students can verify their answers using the standard series too.
![\ln(1 + \sin 3x) \approx \ln( 1 + (3x) - \frac{1}{6}(3x)^3 ) \approx (3x) - \frac{1}{6}(3x)^3 + \frac{1}{2}[(3x) - \frac{1}{6}(3x)^3]^2 + \frac{1}{3} [ (3x) - \frac{1}{6}(3x)^3]^3 + \ldots](http://theculture.sg/wp-content/ql-cache/quicklatex.com-c9df2d8d806f24114a6cb5c4b497b927_l3.png "Rendered by QuickLaTeX.com")
(i) [Maximum marks: 4]
We can first convert all the given complex numbers to exponential form.
*Another approach is to straightaway solve for 
and 
.
(ii) [Maximum marks: 3]
, and
![z_4 = \sqrt{2} \bigg[ \cos (-\frac{11\pi}{12} + i \sin (- \frac{11\pi}{12})\bigg]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-acf5833f07cffc3ad0a33fa991d8c275_l3.png "Rendered by QuickLaTeX.com")
* Another approach is to observe that 
Note/ Comment: This can be tedious if the student did not use exponential form to get around things. For (ii), the question has stated “possible values” which is a hint that there is more than one answer to be expected. Aside from it, students should use GC to check their answers.
(i) [Maximum marks: 2]
We have that 
, so 
is parallel to 
and 
where 
is a scalar.
(ii) [Maximum marks: 3]
R is a set of points lying on a line that passes through position vector 
and is parallel to direction vector 
, where 
is a scalar parameter.
(iii) [Maximum marks: 4]
R is a set of point lying on a plane that passes through position vector 
and is perpendicular to normal vector 
, where 
units is the shortest displacement R is from the origin.
Note/ Comment: Quite a standard question, from the specimen paper and also from 2017 A’levels paper. Students should be able to answer this comfortably.
By comparing the coefficients, 
Other root 
and 
and 
Note/ Comment: Actually this question did not prohibit the GC, so the last part could be done easily.
(i) [Maximum marks: 1]
(ii) [Maximum marks: 4]
![= \bigg[ x(2x + \frac{1}{4}\cos 4x) \bigg]_0^{\frac{\pi}{2}} - \int_0^{\frac{\pi}{2}} (2x + \frac{1}{4}\cos 4x) ~dx](http://theculture.sg/wp-content/ql-cache/quicklatex.com-465f322875173f7020db7e17e3884b19_l3.png "Rendered by QuickLaTeX.com")
![\frac{\pi}{2} ( \pi + \frac{1}{4}) - \bigg[ x^2 + \frac{1}{16} \sin 4x \bigg]_0^{\frac{\pi}{2}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-3e99b9d4402b5cff8022396ca5a9f8c5_l3.png "Rendered by QuickLaTeX.com")
(iii) [Maximum marks: 4]
![= \bigg[ 4x + \frac{1}{2}\cos 4x + \frac{1}{2}x - \frac{\sin 8x}{16} \bigg]_0^{\frac{\pi}{2}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-aee2a61bf195920cc0d469fb2979df47_l3.png "Rendered by QuickLaTeX.com")
Note/ Comment: Students should use GC to check their answers.
(a)(i) [Maximum marks: 2]
(a)(ii) [Maximum marks: 3]
![= \frac{50}{2}[8 + 49(1.5)] - \frac{20}{2}[8 + 19(1.5)]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-ec643004a403f3f0654a11f7b60b27f1_l3.png "Rendered by QuickLaTeX.com")
(b)(i) [Maximum marks: 2]
(b)(ii) [Maximum marks: 5]
Smallest possible 
.
Note/ Comment: Standard question.
(i) [Maximum marks: 1]
Consider the lines 
and 
, since the gradient 
, where 
is the angle the line makes with the horizontal and the two lines and are perpendicular, i.e., 
radians spaced from each other. We have that 
.
(ii) [Maximum marks: 3]
Since 
, required set 
(iii) [Maximum marks: 3]
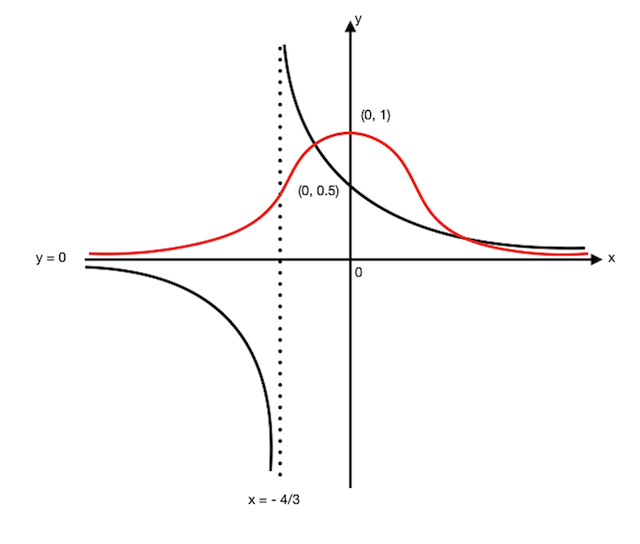
Note: Right side of the graph. The asymptote is y=0, I do not know why wordpress cut it off. 🙁
(iv) [Maximum marks: 5]
Using GC, 
![= \bigg[ \tan^{-1} x - \frac{2}{3} \ln \vert 4 + 3x \vert \bigg]_{-0.5}^2](http://theculture.sg/wp-content/ql-cache/quicklatex.com-ac7cc8e0beb8cc94bbf2f4b9d7913987_l3.png "Rendered by QuickLaTeX.com")
(i) [Maximum marks: 2]
(ii) [Maximum marks: 4]
, where 
is an arbitrary constant.
In the long run, 
, The number of sheep will decrease and approach 0.
(iii) [Maximum marks: 2]
(iv) [Maximum marks: 4]
where is an arbitrary constant.
(v) [Maximum marks: 2]
In the long run, 
Note/ Comment: This question is quite difficult to interpret, but once you understand, it should be manageable.
(i) [Maximum marks: 3]
Let 
and 
, then 
(ii) [Maximum marks: 3]
Differentiate with respect to ,
Let 
(iii) [Maximum marks: 1]
There are other external factors such as the strength of the kick, or wind, etc.
Note: I personally cannot think of a mathematical reason. Please share with me if you do. So I guess anything logical is fine.
(iv) [Maximum marks: 3]
.
When 
(v) [Maximum marks: 2]
I wanna read the comment
you will have better luck at reddit
For the DE question, if i got the equation wrong but the steps in ii correct and deduced that overtime population approaches 0, will i get any mark.
you should. But the model will probably be wrong since math in general does not carry ecf.
does a wrong DE but correct way of solving DE get marks, thanks!
Given the marks distribution for the question, quite tough.. :/ Since the method to solve the DE was variable separable.
regarding question 2, if i did all steps correctly just during differentiation i carelessly left out the dy dx on the product side of the equation, will there be ecf? or will the 6 marks just fly away like that 🙁 thank you for your reply and the answers!
it won’t just fly away. if your method to find tangents, etc are correct. there will be marks.