Introduction to Brownian Motion

Lets look at brownian motion now. And yes, its the same as what our high school teachers taught about the particles moving in random motion. Here, we attempt to give it a proper structure and definition to work with.

A Brownian Motion is a random process $\{ X_t : t \ge 0 \}$ with parameters $(\mu, \sigma)$ if
For $0 \textless t_1 \textless t_2 \textless \ldots \textless t_{n-1} \textless t_n$ , $(X_{t_2} - X_{t_1}), (X_{t_3} - X_{t_2}), \ldots, (X_{t_n} - X_{t_{n-1}})$ are mutually independent. This is often called the independent increments property.
For $s > 0, X_{t+s} - X_t \sim \mathrm{N} ( \mu s, \sigma^2 s)$
$X_t$ is a continuous function of t.
We say that $X_t$ is a $\mathrm{B} (\mu, \sigma)$ Brownian motion with drift $\mu$ and volatility $\sigma$ .

For the special case of $\mu = 0$ and $\sigma = 1$ , we have a standard Brownian motion. We can denote it with $W_t$ and assume that $W_0 = 0$
If $X_t \sim \mathrm{B}(\mu, \sigma)$ and $X_0 = x$ then $X_t = x + \mu t + \sigma W_t$ where $W_t$ is a standard brownian motion. Thus, $X_t \sim \mathrm{N}(x+\mu t, \sigma^2 t)$

Random Paths of Brownian Motion. Source: Columbia University

The next concept is important in finance, that is, Information Filtrations.
For any random process, we will use $\mathcal{F}_t$ to denote the information available at time t.
– the set $\{\mathcal{F}_t\}_{t \ge 0}$ is then the information filtration.
– $\mathbb{E}[.|\mathcal{F}_t]$ denotes an expectation conditional on time t information available.

Note: The independent increment property of Brownian Motion implies that any function of $W_{t+s} - W_t$ is independent of $\mathcal{F}_t$ and that $(W_{t+s}-W_t) \sim \mathrm{N}(0,s)$ .

So let us do a bit of math to obtain $\mathbb{E}_0[W_{t+s}W_s]$ for instance.

Using condition expectation identity, we have
$\mathbb{E}_0 [W_{t+s}W_s]$
$= \mathbb{E}_0 [(W_{t+s} - W_s + W_s)Ws]$
$= \mathbb{E}_0 [(W_{t+s}-W_s)W_s] + \mathbb{E}_0 [{W_s}^2]$
$= \mathbb{E}_0 [\mathbb{E}_s[(W_{t+s} - W_s)W_s]] + s$
$= \mathbb{E}_0 [W_s \mathbb{E}_s[(W_{t+s} - W_s)]] + s$
$= \mathbb{E}_0 [W_s 0] + s$
$= 0 + s$
$= s$

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for almost two decades. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Showing 3 comments

pingbacks / trackbacks

Geometric Brownian Motion – The Culture
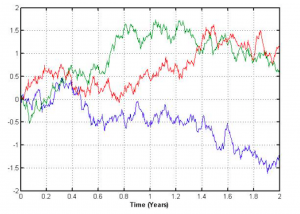
[…] Introduction to Brownian Motion – The Culture on Conditional Expectations and Variances […]
February 6th, 2016 12:17 PM
Introduction to Stochastic Calculus – The Culture
[…] the continuous-time model, will be the filtration generated by the stochastic processes (usually a brownian motion, ), based on the model’s […]
May 13th, 2016 09:45 AM
Review of Basic Probability – The Culture
[…] Introduction to Brownian Motion […]
May 13th, 2016 11:48 PM

Cart

Introduction to Brownian Motion

Leave a Comment
Cancel reply

Introduction to Brownian Motion

Leave a Comment Cancel reply

Leave a Comment
Cancel reply