Will it ever converge?

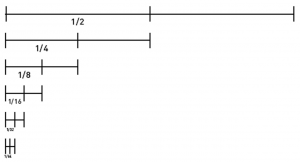
If KS travels half the distance to the bus stop for every move, will he ever reach the bus stop?

The answer is that I will never reach the bus stop, but could make arbitrarily close to it. This excellent example of an geometric progression is called the dichotomy paradox.

Credits: www.learner.org

We all know that to prove that a GP converges, show . But I’ve heard a handful of students asking why. So today, lets break it down together.

The very idea of |r|

If , it’s obvious that my GP converges.

If or , we can suggest that r is simply a decimal number less than +/-1, then r^n will simply get smaller as n increases, until it is arbitrarily so small that it’s almost 0. Even if we say r = 0.99999, 0.99999^1000 will not give you 1, it instead, gives you a really small number.

I hope these helps to clear the air for this condition. A food for thought, if I am not given the value of r, will I still be able to prove if it converges? 🙂