All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
Two direction vectors on the plane are ![]() and
and ![]()
Normal vector of plane, 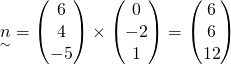
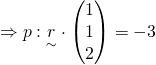
![]()
(ii)
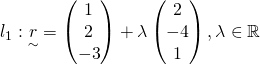
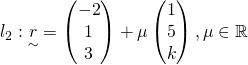
Since both lines intersect, 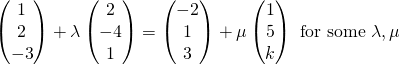
![]()
![]()
![]()
Using GC, ![]()
(iii)
Since 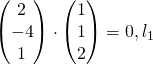 is parallel to plane p.
is parallel to plane p.
Since 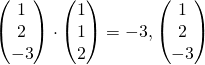 lies on plane p.
lies on plane p.
Thus, ![]() lies in p.
lies in p.
![Rendered by QuickLaTeX.com [\begin{pmatrix}-2\\1\\3\end{pmatrix} + \mu \begin{pmatrix}1\\5\\k\end{pmatrix}] \cdot \begin{pmatrix}1\\1\\2\end{pmatrix} = -3](http://theculture.sg/wp-content/ql-cache/quicklatex.com-79d51394ae6d5d4df89c541c7187af39_l3.png)
![]()
Required coordinate ![]()
(iv)
Required acute angle ![Rendered by QuickLaTeX.com =sin^{-1} \frac{\begin{pmatrix}1\\5\\-7\end{pmatrix}] \cdot \begin{pmatrix}1\\1\\2\end{pmatrix}}{\sqrt{75} \sqrt{6}} = 22.2^{\circ}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-4edc56c742bbb5cf42667b03ef701d4e_l3.png)
KS Comments:
This question was well attempted. For (iii), some students might find it easier to plug the entire equation of ![]() into the equation of plane p and show. Aside from being careless in the vector manipulations, there were not much mistakes.
into the equation of plane p and show. Aside from being careless in the vector manipulations, there were not much mistakes.

[…] Question 11 […]