All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
![]()
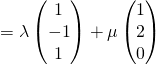
Area ![]()
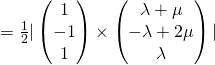
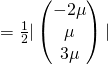
![]()
![]()
![]()
(ii)
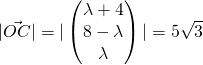
![]()
![]()
Thus required coordinates are ![]() and
and ![]()
KS Comments:
Students just got to be careful when doing the cross product since there are unknowns.
