All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1: ![]()
Question 2: ![]()
Question 3: 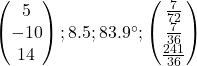
Question 4: ![]()
Question 5: A and B, or A and D; B and C; A and B, or A and D; not independent
Question 6: ![]()
Question 7: ![]()
Question 8: ![]() , reject
, reject ![]()
Question 9: ![]()
Question 10: ![]()
(a)
Method 1: Algebraic![]()
![]()
![]()
![]()
![]()
![]()
Method 2: Graphical
(b)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(a)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (shown)
(shown)
(b)
When ![]()
![]()
(c)(i)![]()
![]()
![]()
![]()
(c)(ii)![]()
![]()
![]()
![]()
(a)![]()
![]()
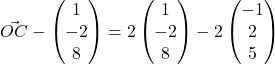
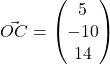
(b)![]()
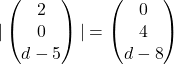
![]()
![]()
![]()
![]()
(c) 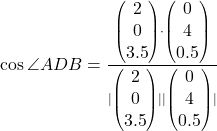
![]()
![]()
(d) Using (b), we recognise that we are inscribing an isosceles triangle with AB as the base in the circle to find the center. We let ![]() be the mid point of AB and
be the mid point of AB and ![]() be the radius of the circle.
be the radius of the circle.
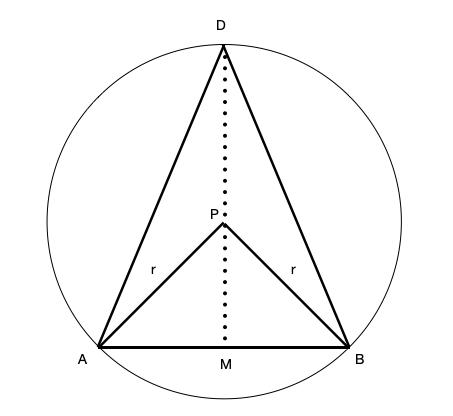
Method 1: Pythagoras’ theorem
From (c), we found that ![]() and
and ![]() .
.
By Pythagoras’ Theorem, ![]()
![]()
![]()
By Pythagoras’ Theorem,![]()
![]()
![]()
![]()
![]()
Thus, the ratio of ![]()
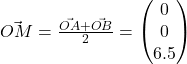
![]()
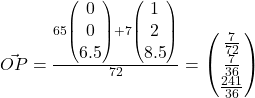
Method 2: Vector equation of a line
We have that 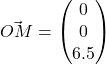 , then
, then 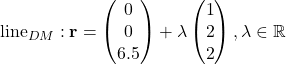
We let 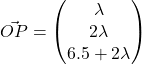 for some
for some ![]() .
.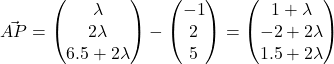
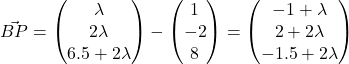
Since ![]() ,
, ![]()
Using GC, we find no solutions. So we should consider DP instead.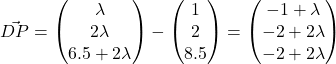
We let ![]()
![]()
Using GC, ![]() . Thus,
. Thus, 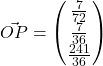
(a)
Using GC, we can find that when ![]() and
and ![]() .
.![]()
![]()
![]()
![]()
![]()
(b)![]()
![]()
Since they intersect, we can equate the ![]() and
and ![]() coordinates, we have
coordinates, we have![]() and
and ![]() .
.![]()
![]()
![]()
![]()
Using GC, ![]() , and
, and ![]() .
.
Thus, ![]() . Since the above cubic equation only has one solution, we can conclude that there are no other solutions for
. Since the above cubic equation only has one solution, we can conclude that there are no other solutions for ![]() for which
for which ![]() and
and ![]() intersect.
intersect.
(c) Using GC, at ![]()
Equation of tangent: ![]()
Since it meet curve D, ![]()
![]()
![]()
Using GC, ![]() or
or ![]() (rejected since this is A)
(rejected since this is A)
The required coordinates are ![]()
![]() and we can observe that
and we can observe that ![]() .
.![]() and we can observe that
and we can observe that ![]() .
.![]() and we can observe that
and we can observe that ![]() .
.![]() and we can observe that
and we can observe that ![]() .
.
(a)(i)A and B are mutually exclusive events. A and D are also mutually exclusive events.
(a)(ii)![]()
![]()
Since ![]() , we have that A and C are independent events.
, we have that A and C are independent events.
Since B is the complement of A and we have the A and C are independent events, then we have that B and C are independent events as well.
(b) We can update the elements.![]() and we can observe that
and we can observe that ![]()
![]() and we can observe that
and we can observe that ![]()
![]() and we can observe that
and we can observe that ![]()
![]() and we can observe that
and we can observe that ![]()
(i) Thus, A and B are mutually exclusive events. A and D are also mutually exclusive events.
(ii)![]()
![]()
Since ![]() , we have that A and C are no longer independent events.
, we have that A and C are no longer independent events.
(a)![]()
![]()
![]()
![]()
![]()
![]()
(b)![]()
![]()
![]()
![]()
![]()
![]()
Solving simultaneously, we find that ![]() and
and ![]()
Thus the required probability ![]()
(a)(i)
Using the GC, product moment correlation coefficient ![]()
(a)(ii)
Using the GC, product moment correlation coefficient ![]()
(b) The model ![]() is a better fit to the data as the magnitude of the product moment correlation coefficient is closer to 1 which suggests a stronger positive linear correlation. Further we observe that the values of
is a better fit to the data as the magnitude of the product moment correlation coefficient is closer to 1 which suggests a stronger positive linear correlation. Further we observe that the values of ![]() increase decreasingly as
increase decreasingly as ![]() increases.
increases.
Using GC, ![]()
(c)
Let ![]()
There are 8.87 million subscriptions in 2024. This estimate is not reliable as ![]() does not fall in the data range of
does not fall in the data range of ![]() .
.
(a)(i)
Let ![]() be the population mean weight of granulated sugar.
be the population mean weight of granulated sugar.
Test ![]()
against ![]()
where ![]() is the null hypothesis and
is the null hypothesis and ![]() is the alternative hypothesis.
is the alternative hypothesis.
(a)(ii)
Since the distribution of the masses of each bag of sugar is unknown, a sample of 10 bag of sugar will not be sufficiently large as it is ![]() for the sample mean to be approximated to a normal distribution by central limit theorem,
for the sample mean to be approximated to a normal distribution by central limit theorem,
The sample collected by the manager will not give a random sample as the chance for each bag to be selected is not equal and selection is not independent of each other. This will give rise to bias.
(b)(i)
Let ![]() denote the sample mean masses of sugar.
denote the sample mean masses of sugar.
We first find that ![]()
Test ![]()
against ![]() at 2.5% level of significance.
at 2.5% level of significance.
Under ![]() , since sample size
, since sample size ![]() is sufficiently large, by central limit theorem
is sufficiently large, by central limit theorem![]() approximately.
approximately.
Test statistic, ![]()
For ![]() to be rejected,
to be rejected,![]()
![]()
![]()
Thus the critical region is ![]()
(b)(ii)
Since ![]() falls in the critical region found in (b)(i), we reject
falls in the critical region found in (b)(i), we reject ![]() at 2.5% significance level and conclude with sufficient evidence that mean mass of sugar are less than 2kg.
at 2.5% significance level and conclude with sufficient evidence that mean mass of sugar are less than 2kg.
(a) Let ![]() denote the length of regular and long planks respectively, in m.
denote the length of regular and long planks respectively, in m. ![]()
Required probability ![]()
(b) Let ![]()
Required probability ![]()
(c) Let ![]()
Expected number of planks ![]()
(d) Let ![]()
![]()
![]()
![]()
Required probability ![]()
(e) Let ![]()
Required probability ![]()
(f) We let ![]() denote the wastage, and since
denote the wastage, and since ![]() , when there is wastage, we observe that the variance of
, when there is wastage, we observe that the variance of ![]() will increase. This will lead to the probability found to be higher.
will increase. This will lead to the probability found to be higher.
(a)(i)
The event that a randomly chosen ornament turns out to be faulty is independent of the event that another randomly chosen ornament turns out to be faulty.
The probability that a randomly chosen ornament turns out to be faulty is constant, throughout the the sample.
(a)(ii)
mean ![]()
variance ![]()
difference ![]()
(a)(iii)
Let ![]() be the number of faulty ornaments, out of 50 ornaments.
be the number of faulty ornaments, out of 50 ornaments. ![]()
Required probability ![]()
(a)(iv)
Let ![]() be the number of days where there are no more than 2 faulty ornaments, out of 5 days.
be the number of days where there are no more than 2 faulty ornaments, out of 5 days. ![]()
Required probability ![]()
(a)(v)
Let ![]() be the number of faulty ornaments, out of
be the number of faulty ornaments, out of ![]() ornaments.
ornaments. ![]()
Required probability ![]()
(b) Let ![]() denote the event that the box is accepted.
denote the event that the box is accepted.
For Lu,![]()
![]()
![]()
For Ming,![]()
![]()
![]()
Consider ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() for
for ![]() .
.
Thus we have that ![]()
[…] 2023 A-level H2 Mathematics (9758) Paper 2 […]
Leave a CommentCancel reply

hello!! would you mind making solutions for H1 math too? thank you lots!! :))
Hi, I did do the stats for my h2 math students to try. Haven’t got time to do the pure math section though.
2023 A-level H1 Mathematics (8865) Paper 2 Suggested Solutions
Hi…When r you uploading the answer for paper 2? Thankz in advanced!
Hello, I just started doing. Had other commitments to attend to the whole day. Will try my best.
Can we expect to see the suggested solutions by next week? Thank you
Hello, I just started doing. Had other commitments to attend to the whole day. Will try my best.
hello! do you mind making the answers for todays h2 math paper 2? thank you 😊
Hello, I just started doing. Had other commitments to attend to the whole day. Will try my best.
hi for the hypo testing qn, is the given s^2 value in your solution = n/n-1 (sample variance)? thank you
hello, nope, we can apply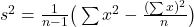 .
.
hi, isn’t that equal to (n/n-1)(sample variance) as well?