Discrete Random Variables

By KS Teng

As usual, definitions first.

The cumulative distribution function (CDF), F(\bullet) of a random variable, X, is defined by
F(x) := P(X \le x)

A discrete random variable, X, has probability mass function (PMF), p(\bullet), if p(x) \ge 0 and for all events A we have P(X \in A) = \sum_{x \in A} p(x)

The expected value of a discrete random variable, X is given by
\mathbb{E} [X] := \sum_i x_i p(x_i)

The variance of an random variable, X, is defined as Var(X) := \mathbb{E} [(X- \mathbb[X])^2] = \mathbb{E}[X^2] - \mathbb{E}[X]^2

Source: mathstatica.com

Source: mathstatica.com

Now we can look at some examples of discrete random variables.

    Binomial Distribution

We say the X has a binomial distribution, that is, X \sim Bin(n, p), if P(X=r) = {n \choose r} p^r (1-p)^{n-r}
For example, X can represent the number of heads in n independent coin tosses, where p = P(head). We have that the mean \mathbb{E}[X] = np and variance Var(X) = np(1-p)

A simpler case of binomial where there is only one event is called the Bernoulli distribution.

I’ll give a simple illustration of binomial model used in finance. This was also used in finance engineering in the beginning.
Suppose a fund manager outperforms the market in a given year with probability p and under performs the market with probability 1 – p. She has a track record of 10 years and has outperformed the market in 8 out of 10 years. We also note that performance in any one year is independent of performance in other years.
From this illustration, we note that there are only two outcomes, she outperforms or underperforms. We can let X be the number of outperforming years. Assuming the fund manager has no skill, X \sim Bin(10, \frac{1}{2}) and we can find P(X \ge 8) to find out the probability that she outperforms at least 8 out of 10 years.
An extension here will be to consider there are M fund managers instead of 1 now.

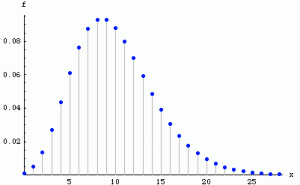
    Poisson Distribution

      We say that X has a Po(\lambda) distribution if
      P(X=r) \frac{{\lambda}^r e^{- \lambda}}{r!}
      \mathbb{E} [X] = \lambda
      Var(X) = \lambda

      Next, we look at Bayes Theorem, also known as “conditional probability” in H2 Mathematics.

      Let A and B be two events for which P(B) \neq 0. Then

      P(A | B)
      = \frac{P(A \cap B)}{P(B)}
      = \frac{P(B | A) P(A)}{\sum_j P(B | A_j) P(A_j)}
      where A_j‘s form a partition of the sample space.

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    Sampling & Survey #6 – Systematic SamplingUniversity Mathematics
    Financial Engineering (I) #2 – Introduction to No ArbitrageUniversity Mathematics